Page 175 - 《软件学报》2025年第12期

5556 软件学报 2025 年第 36 卷第 12 期

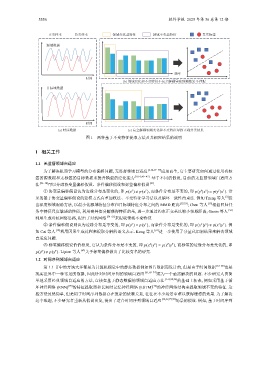
正类样本 负类样本 领域变化基特征 领域不变基特征 真实标签
源域数据

频率
时间
(b) 领域变化和不变特征不完全解耦导致预测效果不理想
目标域数据

时间
(a) 时序数据 (c) 完全解耦领域变化和不变特征导致正确分类结果
图 1 两种基于不变特征提取方法及其相应结果的说明

1 相关工作

1.1 无监督领域自适应
为了解决机器学习模型的分布偏移问题, 无监督领域自适应 [1,12,17−39] 应运而生, 它主要研究如何通过使用有标
签的源数据和无标签的目标数据来提升模型的泛化能力 [9,10,40−45] . 基于不同的假设, 目前的无监督领域自适应方
法 [46−50] 可以分成协变量偏移假设、条件偏移假设和标签偏移假设 [51] .
( ) ( ) ( S S ) T T
S
T
① 协变量偏移假设认为边缘分布是变化的, 即 p x , p x , 而条件分布是不变的, 即 p y |x = p(y |x ). 常
见的基于协变量偏移假设的建模方式有重加权法、不变特征学习法以及循环一致性约束法. 例如 Tzeng 等人 [3] 提
出深度领域混淆方法, 以最小化源域特征分布和目标域特征分布之间的 MMD 距离 [52,53] ; Chen 等人 [19] 根据回归任
务中特征尺度敏感的性质, 利用奇异值分解获得特征的基, 进一步通过约束正交基以缩小领域距离; Ganin 等人 [54]
利用生成对抗网络思路, 提出了对抗网络 [54−61] 来提取领域不变特征.
( ) ( ) ( S S ) T T
T
S
② 条件偏移假设则认为边缘分布是不变的, 即 p y = p y , 而条件分布是变化的, 即 p x |y , p(x |y ). 例
如 Cai 等人 [18] 利用因果生成过程来提取分解的语义表示. Kong 等人 [61] 进一步使用了分量式识别结果来解决领域
自适应问题.
( S S ) T T
③ 标签偏移假设恰恰相反, 它认为条件分布是不变的, 即 p x |y = p(x |y ), 而标签的边缘分布是变化的, 即
( ) ( ) [62]
T
p y S , p y . Lipton 等人 关于标签偏移做出了比较有名的研究.
1.2 时间序列领域自适应
第 1.1 节中的方法大多都是为计算机视觉中的静态数据例如图片数据而设计的, 但是由于时间数据 [63–68] 也是
现实世界中一种常见的数据, 因此针对时间序列的领域自适应 [61,69–74] 成为一个亟需解决的问题. 不少研究人员简
单地采用经典领域自适应的方法, 直接在基于静态数据的领域自适应方法 [1–3,34,36] 的基础上拓张, 例如采用基于循
环神经网络 (RNN) [75] 的特征提取器和长短时记忆神经网络 (LSTM) [76] 的神经网络结构来提取领域不变的特征. 这
些方法虽然简单, 但是碍于时间序列数据存在复杂的依赖关系, 往往在不少场景中难以获得理想的效果. 为了解决
这个难题, 不少研究者重新从假设出发, 提出了适合时间序列领域自适应 [30,32,77,78] 场景的假设. 例如, 基于时间序列