Page 456 - 《软件学报》2025年第5期
P. 456
2356 软件学报 2025 年第 36 卷第 5 期
而变化. 同时, 可以在 2 个数据集上观察到在相同 minPts 取值下, ICFPM 算法相对于其他 4 种算法消耗时间总是
最少, 并且 Naive-NoPrune 算法要好于 Naive 算法, 与时间复杂度分析结果相同. 当 minPts 取 8 时, Naive 算法要
比 ICFPM 多消耗约 100 倍时间.
10 3
10 3
Time (s) Time (s)
10 2
10 2
8 10 12 14 16 8 10 12 14 16
minPts minPts
(a) Value-Inc (b) MBA
Naive Naive-NoPrune Naive-T1 Naive-T2 ICFPM
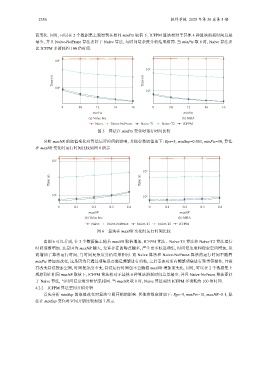
图 5 算法在 minPts 变化时运行时间比较
分析 maxNR 的取值变化对算法运行时间的影响, 其他参数取值如下: Eps=5, minSup=0.003, minPts=10, 算法
在 maxNR 变化时运行时间比较如图 6 所示.
10 3
10 3
Time (s) Time (s)
10 2
10 2
0 0.1 0.2 0.3 0.4 0 0.1 0.2 0.3 0.4
maxNR maxNR
(b) Value-Inc (b) MBA
Naive Naive-NoPrune Naive-T1 Naive-T2 ICFPM
图 6 算法在 maxNR 变化时运行时间比较
由图 6 可以看到, 在 2 个数据集上随着 maxNR 取值增加, ICFPM 算法、Naive-T1 算法和 Naive-T2 算法运行
时间逐渐增加. 这是因为 maxNR 越大, 允许存在的噪点越多, 产生更多候选项集, 时间复杂度和搜索空间增加, 从
而增加了算法运行时间, 与时间复杂度分析结果相同. 而 Naive 算法和 Naive-NoPrune 算法的运行时间不随着
minPts 增加而改变, 这是因为只通过项集是否满足频繁进行剪枝, 之后需要对所有频繁项集进行聚类等操作, 并没
有改变算法搜索空间, 时间复杂度不变, 算法运行时间也不会随着 maxNR 增加而变化. 同时, 可以在 2 个数据集上
观察到在相同 maxNR 取值下, ICFPM 算法相对于其他 4 种算法消耗时间总是最少, 并且 Naive-NoPrune 算法要好
于 Naive 算法, 与时间复杂度分析结果相同. 当 maxNR 取 0 时, Naive 算法要比 ICFPM 多消耗约 100 倍时间.
4.2.2 ICFPM 算法空间开销分析
首先分析 minSup 的取值改变对算法空间开销的影响. 其他参数取值如下: Eps=5, minPts=10, maxNR=0.1, 算
法在 minSup 变化时空间开销比较如图 7 所示.