Page 307 - 《软件学报》2025年第5期

刘振亚 等: SM2 数字签名算法的两方门限计算方案框架 2207

序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

s = (1+d) −1 (k +r)−r d 1 d 2 k 2 +d 1 k 1 +(d 1 d 2 −1)r d 1 d 2 +d 1 k 1 +(d 1 d 2 −1)r d 1 (k 2 +k 1 )+(d 1 d 2 −1)r d 1 d 2 +d 1 d 2 k 2 +d 1 k 1 +(d 1 d 2 −1)r d 1 d 2 +d 1 (k 2 +k 1 )+(d 1 d 2 −1)r d 1 d −1 +d 1 d 2 k 2 +d 1 k 1 +(d 1 d 2 −1)r d 1 +d 1 d 2 k 2 +d 1 k 1 +(d 1 d 2 −1)r d 1 d 2 k 2 +d 2 k 1 +(d 1 d 2 −1)r 1 d 1 d 2 k 2 +d 2 k 1 +(d 1 d 2 −1)r 1 d 1 (k 2 +d 1 k 1 )+(d 1 d 2 −1)r d 1 d 2 +d 1 d 2 k 2 +d 2 k 1 +(

2 2 2 2 2 ( k 2 +d −1 k 1
2 2 d 1

) 2 ) ) ) ) ) ) 2 ) ) )
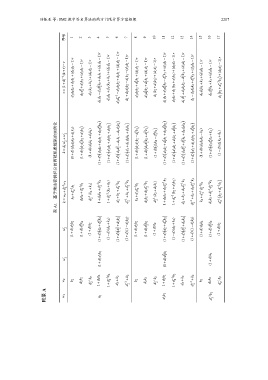
表 A1 基于乘法密钥拆分的两随机数框架的实例化
)
1 1 1 ) 1 1 1 )
2 +w ′ 2 2 1 1 2
k = d 1 w ′ (1+d)(d 1 d 2 k 2 +d 1 k 1 ) (1+d) ( d 1 d 2 k 2 +d 1 k 1 (1+d)(d 1 k 2 +d 1 k 1 ) (1+d) ( d 1 d 2 +d 1 k 1 +d 1 d 2 k 2 (1+d) ( d 1 d 2 +d 1 k 2 +d 1 k 1 (1+d) ( d 1 d 2 +d 1 k 1 +d 1 d 2 k 2 2 (1+d) ( d 1 +d 1 d 2 k 2 +d 1 k 1 (1+d) ( d 1 d 2 k 2 +d 2 k 1 (1+d) ( d 1 d 2 k 2 +d 2 k 1 (1+d) ( d 1 k 2 +d 2 k 1 (1+d) ( d 1 d 2 +d 2 k 1 +d 1 d 2 k 2 (1+d) ( d 1 d 2 +d 1 k 2 +d 2 k 1 (1+d) ( d 1 d 2 +d 2 k 1 +d 1 d 2 k

k = w 2 +d −1 w 1 2 k 2 +d −1 k 1 2 d 2 k 2 +d −1 k 1 2 d −1 (k 2 +k 1 ) 1+d 2 k 2 +d −1 k 1 2 1+d −1 (k 2 +k 1 ) 2 d 2 +k 2 +d −1 k 1 2 d −1 +k 2 +d −1 k 1 2 k 2 +d 1 d −1 k 1 2 d 2 k 2 +d 1 d −1 k 1 2 d −1 (k 2 +d 1 k 1 ) 1+d 2 k 2 +d 1 d −1 k 1 2 1+d −1 (k 2 +d 1 k 1 ) d 2 +k 2 +d 1 d −1 k 1 2 d −1 +k 2 +d 1 d −1 k 1 2 k 2 +d −1 d −1 k 1 2 1 d 2 k 2 +d −1 d −1 k 1 2 1 ) d −1 ( k 2 +d −1 k 1 1

2 2 2 2 2 2

) 2 ) ) 2 )
(1+d)d 2 k 2 (1+d)d 2 k 2 2 (1+d)k 2 (1+d)(d 2 +k 2 ) 2 (1+d)(1+d 2 k 2 ) (1+d)d 2 k 2 (1+d)d 2 k 2 2 (1+d)k 2 (1+d)(d 2 +k 2 ) 2 (1+d)(1+d 2 k 2 ) (1+d)d 2 k 2 (1+d)d 2 k 2 2 (1+d)k 2
2
w ′ (1+d) ( d 2 +d 2 k 2 (1+d) ( d 2 +d 2 k 2 (1+d) ( d 2 +d 2 k 2 (1+d) ( d 2 +d 2 k 2

(1+d)d 1 k 1 (1+d)d 2 k 1 1 (1+d)k 1
1
w ′

w 2 k 2 d 2 k 2 d −1 k 2 1+d 2 k 2 1+d −1 k 2 2 d 2 +k 2 d −1 +k 2 k 2 d 2 k 2 d −1 k 2 1+d 2 k 2 1+d −1 k 2 2 d 2 +k 2 d −1 +k 2 k 2 d 2 k 2 d −1 k 2
2 2 2
2 2

A
w 1 k 1 d 1 k 1 d −1 k 1
1
附录