Page 383 - 《软件学报》2024年第4期

徐怡 等: 基于遗传算法的划分序乘积空间问题求解层选择 1961

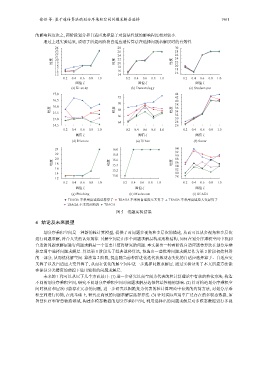
的影响程度次之, 两阶段划分和自适应选择算子对算法性能的影响程度相对较小.
通过上述实验结果, 说明了所提两阶段自适应遗传算法在选择问题求解层时的有效性.

24 28 30
23 26 28
22 24 26
粒度 21 粒度 22 粒度 24
20
22
19
20
18 18 20
17 18
16 16 16
15 14
0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0
阈值 ζ 阈值 ζ 阈值 ζ
(a) Kr-vs-kp (b) Dematology (c) Student-por
17.0 44
72 42
16.5 40
70 38
16.0 36
粒度 15.5 粒度 68 粒度 34
66 32
15.0 30
64 28
14.5 26
0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0
阈值 ζ 阈值 ζ 阈值 ζ
(d) Divorce (e) Urban (f) Sonar
24 16.0 94
92
22 15.8 90
粒度 20 粒度 15.6 粒度 88
86
18
15.4
16 84
82
15.2
14 80
15.0 78
12
0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0
阈值 ζ 阈值 ζ 阈值 ζ
(g) Phishing (h) Mushroom (i) SCADI
TSAGA 不采用自适应选择算子 TSAGA 不采用自适应交叉算子 TSAGA 不采用自适应大变异算子
TSAGA 不采用两阶段 TSAGA
图 5 消融实验结果

4 结论及未来展望

划分序乘积空间是一种新的粒计算模型, 提供了对问题多视角和多层次的描述, 从而可以从多视角和多层次
进行问题求解, 符合人类的认知规律. 其解空间是由多个问题求解层构成的格结构, 如何在划分序乘积空间中找到
合适的问题求解层进行问题求解是一个重要且值得研究的问题. 本文提出一种两阶段自适应遗传算法在划分序乘
积空间中选择问题求解层. 算法第 1 阶段基于经典遗传算法, 预选出一些优秀问题求解层作为第 2 阶段初始种群
的一部分, 从而优化解空间. 算法第 2 阶段, 提出随当前种群进化迭代次数动态变化的自适应选择算子、自适应交
叉算子以及自适应大变异算子, 从而在优化的解空间中进一步选择问题求解层. 通过实验证明了本文所提方法能
在保证分类精度的前提下选出较粗的问题求解层.
未来的工作可以从以下几个方面展开: (1) 进一步研究以商空间为代表的粒计算理论中有效的粒化方法, 构造
不同的划分序乘积空间, 研究不同划分序乘积空间对问题求解层选择算法性能的影响. (2) 针对构造划分序乘积空
间时视角和层次可能存在冗余的问题, 进一步研究以粗糙集为代表的粒计算理论中有效的约简方法, 对划分序乘
积空间进行约简, 在此基础上, 研究更高效的问题求解层选择算法. (3) 针对实际应用中广泛存在的多模态数据, 如
智慧医疗和智慧物流领域, 构建多模态数据的划分序乘积空间, 利用选择出的问题求解层对多模态数据进行多视