Page 126 - 《软件学报》2021年第10期

3098 Journal of Software 软件学报 Vol.32, No.10, October 2021

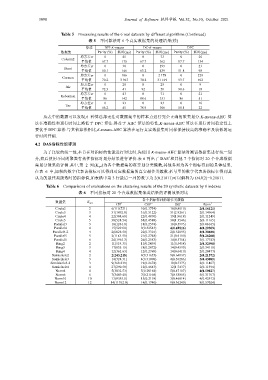
Table 5 Processing results of the 6 real datasets by different algorithms (Continued)
表 5 不同算法对 6 个真实数据集的处理结果(续)
算法 DPI-K-means DC-K-means DPC
数据集 Purity (%) 耗时(ms) Purity (%) 耗时(ms) Purity (%) 耗时(ms)
均方差 0 45 0 73 0 26
Column2
平均值 67.7 175 67.7 162 87.7 134
均方差 0 38 0 195 0 23
Heart
平均值 60.1 146 63.2 439 51.8 98
均方差 0 106 0 2 178 0 229
German
平均值 70.2 3 967 70.2 31 169 93.7 692
均方差 0 28 0 25 0 9
Iris
平均值 72.3 41 92 50 90.6 18
均方差 0 43 0 71 0 21
Haberman
平均值 86 142 88.6 151 86 51
均方差 0 23 0 23 0 16
Tae
平均值 66.2 45 78.9 106 80.1 22
从表中的数据可以发现,6 种算法都无法对数据集中的样本点进行完全正确的聚类划分.K-means-AHC 算
法在准确性和运行时间上略低于 DPC 算法.得益于 AHC 算法的特性,K-means-AHC 算法在运行时间稳定性上
要优于 DPC 算法.与其他算法相比,K-means-AHC 算法在运行真实数据集时同样保持较高的准确率及较低的运
行时间开销.
4.2 DAS指标性能评测

为了比较的统一性,本节在对指标的性能进行对比时,先使用 K-means-AHC 算法对测试数据集进行统一划
+
分,然后使用不同的聚类有效性指标对划分结果进行评价.表 6 列出了 DAS 和其他 7 个指标对 20 个合成数据
集划分效果的评测.其中,第 2 列(K opt )为各个数据集的真实划分类簇数,其他各列为各个指标得到的具体结果.
在表 6 中,加粗的数字代表该指标可以得到对应数据集的真实最佳类簇数.括号里的数字代表各指标在得到其
认为的最佳类簇数时的指标值,如表格中第 3 行最后一列的数字为 2(0.21811)可以解释为 DAS(2)=0.21811.
Table 6 Comparisons of evaluations on the clustering results of the 20 synthetic datasets by 8 indexes
表 6 不同指标对 20 个合成数据集聚类结果的评测效果对比
各个指标得到的最佳类簇数
数据集 K opt +   +
CH COP DB Dunn
Circle2 2 6(110.721) 10(0.3754) 10(0.8010) 2(0.16121)
Circle3 3 31(1892.8) 31(0.3122) 31(2.9261) 2(0.14964)
Circle4 4 22(308.60) 22(0.4870) 19(1.9618) 2(0.11249)
Circle5 5 38(528.54) 38(0.4588) 38(1.3546) 2(0.11165)
Parallel3 3 18(1261.0) 18(0.2574) 18(0.5993) 2(0.06165)
Parallel4 4 15(529.68) 9(0.32543) 4(0.69816) 4(0.29309)
Parallel4-2 4 2(6028.50) 22(0.3316) 2(0.52095) 4(0.30488)
Parallel5 5 2(1143.50) 21(0.2748) 21(0.6100) 5(0.26208)
Parallel6 6 24(1965.3) 24(0.2583) 14(0.5764) 3(0.17743)
Ring2 2 11(519.35) 11(0.2459) 11(0.5458) 2(0.32998)
Ring3 3 17(835.15) 18(0.2072) 14(0.4590) 2(0.34110)
Ring4 4 12(361.63) 12(0.2769) 14(0.6410) 2(0.20477)
Semicircle2 2 2(243.218) 9(0.31655) 9(0.64037) 2(0.21572)
Semicircle3 3 14(724.31) 4(0.31008) 4(0.56286) 3(0.43885)
Semicircle3-2 3 9(368.639) 19(0.2674) 19(0.5375) 2(0.11467)
Semicircle4 4 27(290.50) 12(0.4843) 12(1.7437) 2(0.11394)
Norm4 4 5(3032.53) 5(0.20164) 5(0.47107) 4(0.59827)
Norm6 6 7(3489.40) 7(0.21160) 7(0.53865) 5(0.31767)
Norm10 10 13(9393.0) 13(0.2119) 3(0.46814) 4(0.42912)
Norm12 12 14(11762.0) 14(0.1740) 9(0.36240) 8(0.57024)