Page 117 - 《软件学报》2021年第8期

龚成 等:一种超低损失的深度神经网络量化压缩方法 2399

的权值数据)量化到 x 比特.
4.1 数据仿真评估
• 实验设置
2
首先,随机生成满足正态分布 N(μ,σ )的 100 000 个数据.分别考量条件参数的变化对量化损失所产生的影
响:(1) 不同的量化位宽;(2) 满足标准差σ=1.0 但均值μ不同的正态分布;(3) 满足均值μ=0,但标准差σ不同的正
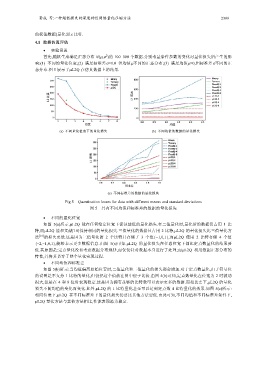
态分布.图 5 展示了μL2Q 在仿真数据上的结果.

(a) 不同量化位宽下的量化损失 (b) 不同均值的数据的量化损失

(c) 不同标准差的数据的量化损失
Fig.5 Quantization losses for data with different means and standard deviations
图 5 具有不同均值和标准差的数据的量化损失

• 不同的量化位宽
如图 5(a)所示,μL2Q 能在任何给定位宽下保证最低的量化损失.在二值量化时,量化后的数据仅占用 1 比
特,而μL2Q 能和文献[18]保持相同的量化损失.三值量化的数据只占用 2 比特,μL2Q 的量化损失比三值量化方
法 [16] 的损失更低.这是因为三值量化的 2 个比特只存储了 3 个值{−1,0,1},而μL2Q 使用 2 比特存储 4 个值
{−2,−1,0,1},能够表示更多数据信息.由图 5(a)可知,μL2Q 的量化损失在任意位宽下都比定点数量化的结果要
低.其原因是:定点量化没有考虑数据分布规律,而仅仅针对数据本身进行了处理;而μL2Q 利用数据正态分布的
特性,并将其贯穿于整个量化实现过程.
• 不同均值和标准差
如图 5(b)所示:当均值偏离原始位置时,二值量化和三值量化的损失都会增加.对于定点数量化,由于符号位
的设置是不支持 1 比特的量化,但仍把这个值放在图中便于比较.由图 5(b)可知,定点数量化在位宽为 2 时波动
很大,但是在 4 和 8 位时表现稳定.这是因为拥有足够的比特数可以表示更多的数据.而相比之下,μL2Q 的量化
损失不随均值的变化而变化.此外,μL2Q 的 1 比特量化甚至可以达到定点数 4 比特量化的效果.如图 5(c)所示:
相同位宽下,μL2Q 在不同标准差下的量化损失仍要比其他方法要低.由此可知,不同均值和不同标准差条件下,
μL2Q 量化方法与其他方法相比,性能表现最为稳定.