Page 114 - 《软件学报》2021年第8期

2396 Journal of Software 软件学报 Vol.32, No.8, August 2021

k
位宽是 k,式(9)中的ϕ空间被分割成宽度为λ的 2 个量化区域;然后将每个量化区域中所有的权值替换为该区域
中的某个最优值.经过标准正态分布的数据空间转换之后,μL2Q 的量化过程可总结为以下 3 个步骤.
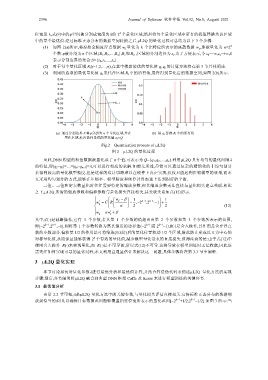
(1) 如图 2(a)所示,将原始全精度浮点数据 w f 量化为 k 个比特位所表示的离散数据 w q ,即被量化为 n=2 k
个数.ϕ被分割为 n 个区域{R 1 ,R 2 ,…,R n },R i 和 R i+1 区域的分割边界为 s i .为了方便表示,令 s 0 =−∞,s n =+∞,S
表示分割边界的集合:S={s 0 ,s 1 ,…,s n }.
(2) 对于每个量化区域 R i (i=1,2,…,n),在其中搜索最优的量化值 q i .q i 的计算方法将在第 3 节具体阐述.
(3) 利用所选取的最优量化值 q i 来代替区域 R i 中的所有值,最终得到量化后的数据空间,如图 2(b)所示.

(a) 通过分割边界 S 将ϕ分割为 n 个量化区域,并在 (b) 用 q i 替换 R i 中的所有值
量化区域 R i 内选择最优的量化值 q i∈Q
Fig.2 Quantization process of μL2Q
图 2 μL2Q 的量化过程

至此,DNN 模型的权值数据被量化成了 n 个值,可表示为 Q={q 1 ,q 2 ,…,q n }.利用μL2Q 具有均匀的量化间隔λ
的特征,即|q 2 −q 1 |=…=|q n −q n−1 |=λ,可以进行相应的求解.如前文所述,尽管可以通过复杂的精细化的非均匀划分
来得到较高的量化模型精度,但是这样的设计思路难以在硬件上真正实现,仅仅只能起到压缩模型的效果,而本
文采用均匀划分的方式,能够在压缩率、模型精度和硬件计算加速上达到很好的平衡.
二值、三值和定点数量化时往往需要特定的缩放参数,但其缩放参数无法直接与量化损失建立关联.相比
之下,μL2Q 所需的缩放参数和偏移参数与量化损失直接相关,其关联关系如式(12)所示.
⎧ ⎛ w − β ⎞ 1 ⎞ ⎛ 1
⎪ w′ = C R ⎜ f − ,2 k − 1 ,2 k − 1 − ⎟ 1 + ⎟
− ⎜
⎨ q ⎜ ⎝ ⎝ α ⎠ 2 ⎟ ⎠ 2 (12)
⎪
⎩ w = q α w′ + q β
其中,C(⋅)是截断操作,它有 3 个参数,若其第 1 个参数的值超出由第 2 个参数和第 3 个参数所表示的范围,
即[−2 k−1 ,2 k−1 ,−1],则将第 1 个参数转换为离其最近的边界值(−2 k−1 或 2 k−1 −1).R(⋅)是舍入操作,其作用是舍弃浮点
数的小数部分.偏移量 1/2 的作用是可将缩放(1/λ倍)后的量化位置移动 1/2 个区域,借此防止形成以 0 为中心的
k
对称量化值,从而保证能够获得 2 个有效的量化值,减少模型量化带来的直接损失.值得注意的是:由于式(12)中
使用舍入操作 R(⋅)来实现量化,而 R(⋅)是不可导的,所以式(12)不可导.这将导致在模型训练时无法收敛,因此还
需关注如何实现可导的量化过程,本文利用直通量估计来解决这一问题,具体步骤将在第 3.3 节中阐释.

3 μL2Q 量化实现

本节讨论如何对量化参数λ进行最优分析和最优值计算,并结合算法伪代码来阐述μL2Q 量化方法的实现
步骤;最后,本节阐明将μL2Q 融合到典型 DNN 框架 Caffe 及 Keras 来进行模型训练的关键环节.

3.1 最优值分析
由第 2.2 节可知,λ是μL2Q 量化方法中的关键参数,与量化损失评估直接相关.它将标准正态分布的数据缩
放到恰当的范围,以确保目标数据范围能够覆盖指定位宽所表示的量化范围[−2 k−1 +1/2,2 k−1 −1/2].如图 3 所示:当