Page 172 - 《软件学报》2020年第11期

3488 Journal of Software 软件学报 Vol.31, No.11, November 2020

本文算法、GMAC、FlowPro 这 3 种算法的表现明显好于其他两种算法.虽然在 mu∈{0.1,0.2,0.25,0.3,0.35}
时,本文算法的 Precision 略低于 GMAC,在 mu∈{0.45,0.5}时,本文算法的 Recall 指标略低于 GMAC 算法,在
mu∈{0.4,0.45,0.5}时,本文算法的 Recall 指标略低于 FlowPro 算法,但只有在 mu=0.3 时,本文算法的 F-score 略
低于 GMAC,在其他 9 个数据集上效果都好于 GMAC 算法.基于模糊相似关系的局部社区发现算法每次选择的
都是与已发现社区内节点隶属度最大的节点,优于其他方法,因此得到了更好的结果.
综上所述,本文算法在 LFR 基准网络上的表现优于其他 4 种算法.
3.3 在真实网络数据集上的仿真实验
上一节我们给出了在仿真网络数据集上的实验结果,本节我们在 4 个公认的用于测试社区发现算法有效
性的真实网络数据集上测试本文算法.这 4 个真实数据集分别为:(1) Karate 数据集 [25] ,该网络是 Zachary 在
1970~1972 年间观察美国一所大学的空手道俱乐部成员之间的关系形成的网络,该网络中包含 34 个节点和 78
[4]
条边,后来因为主管节点 34 和教练节点 1 之间发生分歧,分裂成两个小型的俱乐部;(2) Football 数据集 ,该网络
是美国 NCAA 大学橄榄球 2000 年秋季常规赛 I~A 分区学校间的比赛网络数据,该网络中包含 115 个节点和 613
条边;(3) Polbooks 数据集 [26] ,该网络是 Krebs 建立的美国政治图书网络,该网络中包含 105 个节点和 441 条
边;(4) DBLP 数据集 [27] ,该网络是一个科学家合作网络,网络中的边表示两人至少合作发表过一篇论文,该网络
中包含 317 080 个节点和 1 049 866 条边.这 4 个网络都具有已知的社区结构.
采取与 LFR 数据集上相同的实验方法,我们以这些网络中的每一个节点作为起始节点,进行一次局部社区
发现实验,在每个网络上重复 n(n 为网络中的节点个数)次实验,以这些实验的平均 Precison 和 Recall 作为每一
个数据集的实验结果.由于 DBLP 数据集节点个数太多,LWP、GMAC、FlowPro 这 3 种算法运行时间过长,在该
数据集上,我们不与这 3 个算法对比.为此,我们增加了与算法 CNWNN [21] 的对比.在 Karate 数据集上,我们设置
q=0.5,实验结果如图 4(a)所示.在 Football 数据集上,我们设置 q=0.4,实验结果如图 4(b)所示.在 Polbooks 数据集
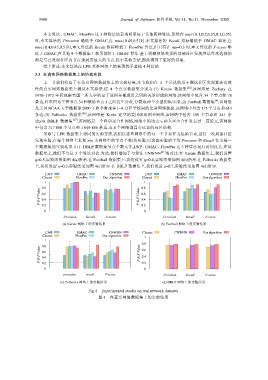
上,我们设置 q=0.3,实验结果如图 4(c)所示.在 DBLP 数据集上,我们设置 q=0.7,实验结果如图 4(d)所示.

LWP GMAC CNWNN LWP GMAC CNWNN
Clauset FlowPro Our algorithm Clauset FlowPro Our algorithm
1 1
0.8 0.8
P-R-F Value 0.6 P-R-F Value 0.6
0.4
0.4
0.2
0 0.2
0
Precision Recall F-score Precision Recall F-score
(a) Karate 网络上的实验结果 (b) Football 网络上的实验结果

LWP GMAC CNWNN Clauset CNWNN Our algorithm
Clauset FlowPro Our algorithm 1
1
0.8
0.8 0.6
P-R-F Value 0.6 P-R-F Value 0.4
0.4
0.2
0 0.2
0
precision recall F-score Precision Recall F-score
(c) Polbooks 网络上的实验结果 (d) DBLP 网络上的实验结果
Fig.4 Experimental results on real network datasets
图 4 在真实网络数据集上的实验结果