Page 171 - 《软件学报》2020年第11期

刘井莲 等:一种基于模糊相似关系的局部社区发现方法 3487

的节点与社区外的节点连接的比例逐渐增加,导致社区发现的难度越来越高.
Table 1 Parameters of LFR
表 1 LFR 参数
参数 含义
n 网络中的节点个数
k 节点平均度
mu 混合参数
k max 节点最大度
C min 最小社区规模
C max 最大社区规模
t 1 节点度的幂率分布指数
t 2 社区规模的幂率分布指数

在实验中,我们以这些网络中的每一个节点作为起始节点,进行一次局部社区发现实验,在每个网络上重复
5 000 次实验,以这些实验的平均 Precison 和 Recall 作为该数据集的实验结果.在实验中,我们设置参数 q 为 0.2,
实验结果如图 3 所示.

1 1
0.8 0.8
Precision 0.6 0.6
Recall
0.4 Clauset 0.4 Clauset
LWP
LWP
GMAC GMAC
0.2 FlowPro 0.2 FlowPro
Our Algorithm Our Algorithm
0 0
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
parameter mu parameter mu
(a) Precision 指标的比较结果 (b) Recall 指标的比较结果

1
0.8
F-score 0.6
0.4 Clauset
LWP
GMAC
0.2 FlowPro
Our Algorithm
0
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
parameter mu
(c) F-score 指标的比较结果
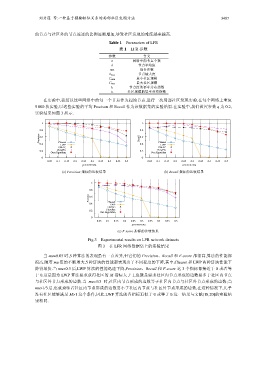
Fig.3 Experimental results on LFR network datasets
图 3 在 LFR 网络数据集上的实验结果
当 mu=0.05 时,5 种算法的表现虽有一点差异,但它们的 Precision、Recall 和 F-score 都很高,算法的性能都
很高.随着 mu 值的不断增大,5 种算法的性能都表现出了不同程度的下降,其中,Clauset 和 LWP 两种算法性能下
降得最快.当 mu>0.3 后,LWP 算法的性能迅速下降,Precision、Recall 和 F-score 这 3 个指标都接近于 0 或者等
于 0.这是因为 LWP 算法要求获得社区的 M 指标大于 1,也就是要求社区内节点形成的边数要多于社区内节点
与社区外节点形成的边数.当 mu=1/3 时,社区内节点形成的边数等于社区内节点与社区外节点形成的边数;当
mu>1/3 后,也就意味着社区内节点形成的边数要小于社区内节点与社区外节点形成的边数,在这种情况下,几乎
没有社区能够满足 M>1 这个条件,因此 LWP 算法的各指标近似于 0 或等于 0.这一结果与文献[18,20]的实验结
果相同.