Page 88 - 《摩擦学学报》2021年第3期

第 3 期 唐玮, 等: 不同尖锐度纹理形状的摩擦触觉感知与表征研究 377

(a) (b) (c)

Fig. 7 Surface deformation of finger during touching (a) sharp shape，(b) round shape，and (c) flat shape
图 7 手指触摸不同纹理形状试样的表面形变示意图

(3)
0.4
F p = σA p
式中：A 为犁削面积；σ为材料的屈服极限. 图7示意了 Sharp shape
Round shape
p
0.3 Flat shape
摩擦感知过程中手指与不同试样的接触. 从图7中可
以看出，手指触摸不同纹理形状试样的皮肤变形程度 0.2
Log, μ
为尖角>圆角>平角，据此可知，触摸过程中犁削摩擦 0.1
力的大小为尖角>圆角>平角.
对于黏弹性材料，变形还会导致材料在滞后恢复 0
过程中产生能量损耗，通常称这部分因素为滞后摩擦.
−0.1
在不考虑黏着作用的情况下，滞后摩擦系数μ 为 −0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4 0.5
h
Log, W/N

p a
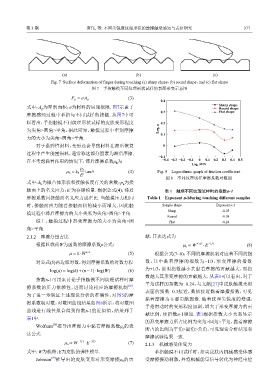
µ h = k h tanδ (4) Fig. 8 Logarithmic graph of friction coefficient
E ′
图 8 不同纹理试样摩擦系数对数图
式中：k 为微凸体形状和接触长度有关的常数；p 为接
h
a
触面上的名义应力；E’为存储模量. 根据公式(4)，滞后 表 1 触摸不同纹理试样时的指数n-1
摩擦系数同接触面名义应力成正比. 当触摸压力相同 Table 1 Exponent n-1during touching different samples

时，接触面应力随着接触面积的减小而增大，因此触 Sample shape Exponent n-1
Sharp -0.05
摸过程中滞后摩擦力的大小关系为尖角>圆角>平角.
Round -0.08
综上，触摸过程中形变摩擦力的大小为尖角>圆 Flat -0.24
角>平角.

2.1.2 摩擦分量占比 献，其表达式为
根据以载荷W为函数的摩擦系数μ公式： µ h ∝ W +1/3 · E −1/3 (8)

µ = k ·W n−1 (5) 根据公式(7~8)，不同的摩擦机制对应着不同的指
对公式(5)两边取对数，得到摩擦系数的对数方程 数，其中黏着摩擦的指数为−1/3，形变摩擦的指数
为+1/3，说明指数越小其黏着摩擦的贡献越大，而指
log(µ) = log(k)+(n−1)·log(W) (6)
数越大其形变摩擦的贡献越大. 从表1可以看出，对于
指数n-1可用来讨论手指触摸不同纹理试样时摩
平角试样的指数为−0.24，与文献[27]中皮肤触摸光滑
[28]
擦系数的压力依赖性，进而讨论相应的摩擦机制 .
表面的指数−0.3接近，数值接近黏着摩擦指数，可见
为了进一步验证上述理论分析的准确性，对图5的摩
黏着摩擦为主要贡献因素. 随着纹理尖锐度的增强，
擦系数取对数，对数图曲线结果如图8所示，将对数图
手指滑动时的变形程度加剧，增大了形变摩擦力的贡
曲线进行线性拟合得到指数n-1的近似值，结果列于
献比例，使指数n-1增加. 表1根据指数大小关系显示
表1中.
的形变摩擦力所占比例为尖角>圆角>平角，黏着摩擦
[28]
Wolfram 推导出摩擦力中黏着摩擦系数μ 的表 所占的比例为平角>圆角>尖角，可见理论分析结果和
a
达公式
摩擦试验结果一致.

µ a ∝ W −1/3 · E −2/3 (7) 2.1.3 机械感受体受力
式中：W为载荷；E为皮肤的弹性模量. 手指触摸不同试样时，指尖皮肤内机械感受体感
[29]
Johnson 推导出的皮肤变形对形变摩擦μ 的贡 受摩擦振动刺激，并将机械能量信号转化为神经电位
h