Page 121 - 《摩擦学学报》2021年第3期

410 摩 擦 学 学 报 第 41 卷

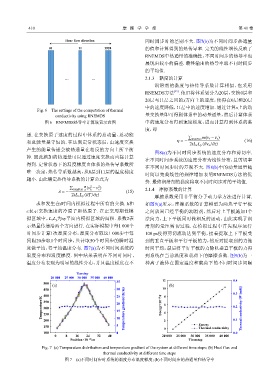
Hear flow direction 同时间步时的差别不大. 图7(b)为不同时间步热通量
01 11 1920 的值和计算得到的热传导率. 完美的线性增长反映了
RNEMDS中热通量的准确性，不同时间步的热导率也
展现出较小的偏差. 最终输出的热导率取不同时间步
的平均值.

… … 2.1.3 黏度的计算
润滑剂的黏度与热传导系数计算相似，也采用
RNEMDS方法 . 依旧将体系划分为20层，交换0层和
[15]
20层与11层之间的x方向上的速度，使得在0层和20层
中的速度降低，11层中的速度增加. 通过计算x上的动

Fig. 6 The settings of the computation of thermal
conductivity using RNEMDS 量交换量即可得到体系中的动量通量，然后计算体系
图 6 RNEMDS热导率计算设置示意图 中的速度分布得到速度梯度，进而计算得到体系的黏
度，即
递. 在交换原子速度的过程中体系的总动量、总动能 ∑
transfers m(v f −v s )
和总能量是守恒的. 在达到定常状态后，由速度交换 η = − (16)
2tL x L y ⟨∂v x /∂z⟩
产生的能量传递会被热通量在相反的方向上所平衡
图8(a)为不同时间步系统的速度分布和剪切率.
掉. 因此施加的热通量可以通过速度交换而直接计算
在不同时间步系统的速度分布为线性分布，且剪切率
得到. 定常状态下的温度梯度由体系的热传导系数所
在不同时间步时的差别不大. 图8(b)中的动量通量随
唯一决定，热传导系数越高，从0层到11层的温度梯度
时间以完美线性的规律增加表明RNEMDS方法的优
越小. 由此确定热传导系数的计算公式为
势. 最终润滑剂的黏度将取不同时间步时的平均值.

∑
m (v −v )
2
2
transfers 2 h c 2.1.4 摩擦系数的计算
λ = − (15)
2tL x L y ⟨∂T/∂z⟩
摩擦系数采用非平衡分子动力学方法进行计算.
求和发生在t时间内模拟过程中所有的交换. h和 如图9(a)所示，摩擦系数的计算模型为两块平行平板
c表示交换速度的冷原子和热原子. 在正交周期性模 之间放置已经平衡的润滑剂，然后对上平板施加1个
拟区域中， L x L y 为xy平面内模拟区域的面积. 系数2表 法向力，上下平板同时做相反的运动，由此实现了润
示热量传递沿两个方向进行. 在实际模拟中每1 000个 滑剂的受压剪切过程. 在模拟过程中首先程序运行
时间步计算1次温度分布，温度分布取这1 000步中每 100 ps使得剪切流动达到平衡，接着提取上下平板受
间隔20步取1个时间步，共计取50个时间步的瞬时温 到的垂直平板和平行平板的力，然后对提取到的力做
度做平均，得平均温度分布. 图7(a)为不同时间系统的 时间平均，最后将平行平板的力除以垂直平板的力得
温度分布和温度梯度. 图中结果表明在不同时间时， 到系统在当前温度和载荷下的摩擦系数. 图9(b)为一
温度分布表现为明显的线性分布，并且温度梯度在不 种离子液体在固定温度和载荷下的不同时间步间隔

Timstep
20 000 25 000 30 000 35 000 40 000
35 12 0.4
500
(a) (b)
450 30 10
400 25 8 0.3
Temperature/K 350 20 Temperature gradient/(K/m) Energy×10 −18 /J 6 4 0.2 Thermal conductivity/[W/(mK)]
300
15
250
200 10 2 0.1
150 5 0 Energy
Thermal conductivity
100 0 0.0
0 8 16 24 32 40 20 000 25 000 30 000 35 000 40 000
−10
Position×10 /m Timestep

Fig. 7 (a) Temperature distribution and temperature gradient of the system at different time steps；(b) Heat flux and
thermal conductivity at different time steps
图 7 (a)不同时间步时系统的温度分布温度梯度；(b)不同时间步的热通量和热导率