Page 120 - 《摩擦学学报》2021年第3期

第 3 期 周峰, 等: 两类润滑剂物性参数和摩擦系数的高通量分子动力学计算 409

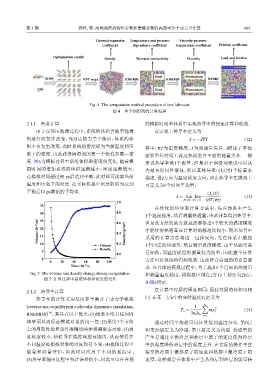
Thermal expansion Temperature and pressure Viscosity-pressure-
coefficient dependence coefficient temperature coefficient Friction coefficient

Optimization results
Density Thermal conductivity Viscosity Load and friction

Heat Momentum
Array NPT relax RNEMD RNEMD NEMD

Heat Momentum

Fig. 4 The computation method procedure of one lubricant
图 4 单个润滑剂的计算流程

2.1.1 密度计算 的模拟时间和体系中实现热导率的快速计算和收敛.
由于在等压弛豫过程中，系统的体积会随着弛豫 在宏观上热导率定义为
的进行而发生改变，当到达热力学平衡后，体系的体 J = −λ∇T (12)
积不再发生改变，此时系统的密度即为当前温度和压 其中： ∇T为温度梯度， 为热通量矢量. J描述了单位
J
强下的密度. 由此获得润滑剂的第一个物性参数—密 面积单位时间上流过热流垂直平面的能量大小. 一般
度. 图5为模拟过程中系统体积和密度的变化. 随着模 来说热导率是1个张量，但是对于润滑剂来说可以认
拟时间的增加系统的体积逐渐减小，密度逐渐增大， 为是各项同性液体，所以其热导率可以用1个标量来
在模拟时间超过90 ps后达到平衡，此时即可读取当前 描述. 设z方向为温度梯度方向，那么热导率在微观上
温度和压强下的密度. 在实际模拟中密度的值为达到 可定义为1个时间平均量：
平衡后10 ps数据的平均值.
⟨J z (t)⟩
λ = lim lim− ⟨∂T/∂z⟩ (13)

1.0 ∂T/∂z→0t→∞
35
在传统的热导率计算方法中，先在体系中产生
30 0.8
1个温度梯度，然后测量热通量，由此计算得到热导率.
Volume×10 −35 /m 3 20 0.4 Density/(g/cm 3 ) 才能使得热通量在计算时的涨落比较小. 而本项目中
25
但是此方法的缺点就是需要给出1个较大的温度梯度
0.6
15
采用的计算方法将这一过程反向，先在体系中施加
10 0.2
Volume 1个固定的热通量，然后测量温度梯度. 由于热通量是
Density
5 已知的，而温度梯度的测量较为简单，因此整个计算
0.0
0 方法可以很快地得到收敛. 由此符合高通量的计算要
0 20 40 60 80 100
−12
Time×10 /s 求. 在具体的模拟过程中，为了施加1个已知的热通量
Fig. 5 The volume and density change during computation 和测量温度梯度，将模拟区域在z方向上划分为20层，
图 5 计算过程中系统体积和密度的变化
如图6所示.
2.1.2 热导率计算 在计算中每层的厚度相同，因此每层的体积也相
热导率的计算采用反向非平衡分子动力学模拟 同. 在某一层 k中的实时温度 定义为
T k
(reverse non-equilibrium molecular dynamics simulation， 1 n k ∑
T k = m i v 2 i (14)
[14]
RNEMDS) ，其具有以下优点：(1)体系中没有任何固 3n k k B i∈k
体壁面从而保证模拟对象的均一性；(2)采用3个方向 通过时间平均就可以计算得到温度分布. 第0层
上的周期性边界条件准确反映体相凝聚态对象；(3)温 和第20层定义为冷层，第11层定义为热层. 热通量的
度梯度较小，热传导在线性响应范围内，从而使得在 产生是通过交换冷层和热层中原子的速度使得冷层
不同温度处模拟对象的密度保持不变；(4)模拟过程中 中的温度降低热层中的温度上升. 在实际的操作中直
能量和动量守恒，因此可以应用于不同的系综中； 接交换冷层中最热原子的速度和热层中最冷原子的
(5)热导率输出过程中统计误差较小，因此可以在合理 速度，这样就会在体系中产生从热层到冷层的能量传