Page 128 - 《摩擦学学报》2020年第5期

第 5 期 赵波, 等: 球形摩擦纳米波浪能发电机的多物理场耦合建模方法研究 683

场. 另外，添加流-固耦合多物理场，将流体选择为层 (a) ×10 V
4
流，结构模块设置为固体力学模块，并将固定几何耦 0.0
合类型设置为全耦合. 至此，在推板、空气和水的相互 −0.2
−0.4
作用下就可以产生具有仿物理造波的随机数值波浪 (b)
−0.6
场，并且和R-TENG产生耦合作用. −0.8
−1.0
2 多物理场耦合模型仿真结果与讨论
Fig. 4 Spatial potential distribution when triboelectric balls
本文模型的几何参数：数值波浪水池的长为80 cm、 rotate through different angles：(a)Simulation results in this
paper；(b) Simulation results in this reference
宽为15 cm，数值波浪水池的水深为5 cm，斜坡的起始
图 4 摩擦起电小球转过不同角度时的空间电势分布:(a)本
点距离推板初始位置55 cm、终止点距离65 cm；球形 文仿真结果；(b)参考文献仿真结果
摩擦纳米发电机的球壳半径为2 cm，电极的半径为
1.5 cm、厚度为0.01 cm、间距为0.1 cm，圆形距离左边界 0.9
t=0 s
20 cm，距离下边界5cm；摩擦起电小球的半径为0.5 cm， 0.8
距离左边界20 cm，距离下边界4.1 cm，以保证初始时 0.7
刻摩擦起电小球和R-TENG的球壳内表面刚好接触； t=1 s 0.6
本文模型对R-TENG部分的网格采用自由三角形网 0.5
格，并设置最大单元大小设置为0.04 cm，其余部分的 0.4
t=2 s
0.3
网格采用自由三角形网格，并设置网格大小为极细化.
0.2
( )
5
5 ∑
推板造波函数的具体表达为 6×sin ×π×t (cm/s). t=3 s 0.1
i
i=1
本模型的仿真总时长为10 s，仿真时间步长为0.001 s，
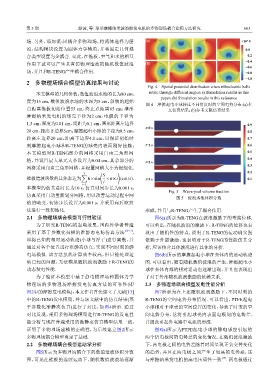
Fig. 5 Wave pool volume fraction
仿真采用自动重新划分网格，用以改善运动过程中网
图 5 波浪水池体积分数
格的畸变，初始步长设置为0.001 s，并采用向后欧拉
法进行一致初始化. 形成，并且与R-TENG产生了耦合作用.
2.1 多物理场耦合模型可行性验证 图6(a)所示为R-TENG在波浪激励下的垂荡位移.
为了研究R-TENG的起电效果，国内外学者普遍 可以看出，在随机波浪的激励下，R-TENG的位移也表
采用了基于参数化扫描的准静态电场仿真方法 [12-13] ， 现出了随机性的特点，说明了R-TENG的运动确实强
即将已知的相对运动轨迹(小球与浮子)进行离散，并 依赖于外部激励，也表明对于R-TENG的性能仿真分
通过对各个位置进行准静态仿真，实现不同时刻的静 析，应该结合具体波况进行具体的分析.
电场模拟. 该方法虽然计算效率较高，但只能处理运 图6(b)所示的摩擦起电小球在壳体内的运动轨迹
动已知的问题，无法模拟随机波浪激励下R-TENG的 图. 可以看出，随着随机数值波浪的产生，摩擦起电小
动态发电性能. 球在壳体内部的相对运动也逐渐出现，并且也表现出
为了验证本模型中基于静电物理场和固体力学 了对于外部随机波浪激励的依赖关系.
物理场的多物理场摩擦发电仿真方法的可靠性(即 2.3 多物理场耦合模型发电性能分析
图2中的摩擦发电模块)，本文作者首先建立了文献[13] 图7所示为在上述随机波浪激励下，不同时刻的
中的R-TENG发电模型，并与该文献中的仿真结果(基 R-TENG的空间电势分布情况. 可以看出，PTFE起电
于参数化准静态仿真)进行了对比，如图4所示. 通过 小球相对于球壳的空间位置的变化，导致了时变的空
对比发现，采用多物理场模型进行R-TENG的发电性 间电势分布，这将引起球壳内表面电极间的电势差，
能分析与现在普遍采用的准静态仿真模型结果一致， 并因此引起外电路中电流的形成.
证明了多物理场建模的正确性，为后续建立图2所示 图8(a)所示为PTFE起电小球的静电感应引起的
多物理场耦合模型奠定了基础. 两个铝电极间的电势差的变化情况. 在随机波浪激励
2.2 多物理场耦合模型运动学分析 下，两电极之间的电势差随着时间呈现正负交替变化
图5所示为多物理场耦合下的数值造波体积分数 的趋势，并且在两电极之间产生了较高的电势差，这
图，可见在推板的连续运动下，随机数值波浪场逐渐 与摩擦纳米发电机的高电压属性一致 . 两电极通过
[19]