Page 106 - 《摩擦学学报》2020年第3期

372 摩 擦 学 学 报 第 40 卷

4
对流场的影响小于惯性力，对扰动的抑制能力减弱， 状态. 取N=1×10 r/min，h=5 μm，h =3 μm，P =2 MPa，
in
g
流速的微小变化容易发展、增强，形成紊乱、不规则的紊流 依据本文参数条件及文献[10]的计算方法，通过流场
流场. 计算分析，可得到v 及端面最大流速v max ，v =85.58 m/s，
r
r
2
2
相关学者 [44-46] 对干气密封性能参数分析计算时， v max =129.59 m/s，由公式v max 2 =v +v 可求出v =97.31 m/s，
r
c
c
选择直接采用公式 (6) 进行干气密封流场流态的类比 带入(8)式，可得：Re =33.75，Re =29.68，ξ=0.025<<1，
p
c
分析：将U类比为平均旋转线速度v，L类比为气膜厚度 根据流动因子判定模型，此时流场流态为层流.
h. 密封几何参数为外径r =77.78 mm，内径r =58.42 mm，
o
i
Re c
−5
3
密度ρ=1.29 kg/m ，黏度μ=1.86×10 Pa·s，膜厚h=3 μm，
4
取转速N=1×10 r/min. 平均线速度计算公式如下：
1 600
Turbulent
( )
r o +r i −3 ξ > 1
N ×π×2 ×10
2
ν = (7) Transition
60 900 region ξ = 1
求解后带入公式(6)得Re=14.84. 9
Laminar ξ = —
16
图7所示为管流中流体流态判定准则，当雷诺数 9
ξ < —
16
Re≤2 300时表示流态为层流，2 300<Re≤4 000时为
0 1 294 2 300
Re p
过渡流动状态，Re>4000时为完全湍流状态. 基于管道
Fig. 8 Flow factor decision model
雷诺数判定模型，同时依据本文中选定参数下的计算
图 8 流动因子判定模型
结果(Re=14.84)可知，即使干气密封转速达到N=1×
6
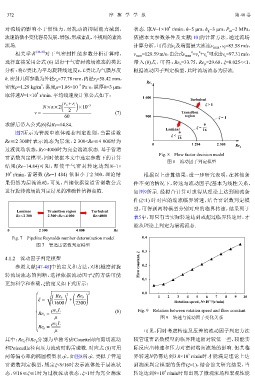
10 r/min，雷诺数 (Re=1 484) 依旧小于2 300，理论结 根据以上计算结果，进一步研究表明，在其他条
果仍然为层流流动，可见，直接依据管道雷诺数公式 件不变的情况下，转速与流动因子ξ基本为线性关系，
进行旋转流场的判定结果的准确性值得商榷. 如图9所示. 经拟合计算可求得从理论上达到湍流条
件(ξ≈1) 时对应的湍流临界转速，结合雷诺数判定模
型，可得到两种模型分别对应的临界转速，结果列于
Laminar Transition region Turbulent
Re≤2 300 2 300<Re≤4 000 Re>4000 表5中，即只有当实际转速达到或超过临界转速时，才
能从理论上判定为湍流流态.
0 2 300 4 000 Re

Fig. 7 Pipeline Reynolds number determination model 0.4
图 7 管道雷诺数判定模型
0.3
4.1.2 流动因子判定模型
参照文献[47-48]中的定义和方法，对机械密封旋 Flow constant, ξ 0.2
转流场流态的判断，选择依据流动因子ξ的方法可能
0.1
更加科学和准确，ξ的定义如下式所示：
√
 ( ) 2 0.0
 ( )2

 Re c Re p 1 2 3 4 5 6 7 8 9 10
ξ = + −4


 Rotation speed, N×10 /(r/min)
 1600 2300





 ρv c L (8) Fig. 9 Relation between rotation speed and flow constant
Re c =


 µ 图 9 转速与流动因子变化关系





 ρv r L

Re p =


µ 可见，同时考虑转速及压差的流动因子判定方法
其中：Re 和Re 分别为单独考虑Couette周向剪切流动 较管道雷诺数模型的临界转速相对较低一些，较能实
c
p
和Poiseuille径向压力流动时的雷诺数. 对应式 (8)可用 际反应出转速和压力对密封端面流场的影响. 但其临
5
两等偏心率的椭圆模型表示，如图8所示. 类似于管道 界转速N仍需达到3.0×10 r/min时才能满足理论上达
雷诺数判定模型，规定ξ<9/16时表示流体处于层流状 到湍流判定模型的条件(ξ≈1)，结合前文研究结果，当
4
态，9/16≤ξ≤1时为过渡流动状态，ξ>1时为完全湍流 转速达到9×10 r/min时即出现了微观流场和宏观性能