Page 201 - 《高原气象》2025年第3期

3 期 韩颂雨等：基于最优插值方法分析的雷达反演三维风场与再分析风场融合试验 759

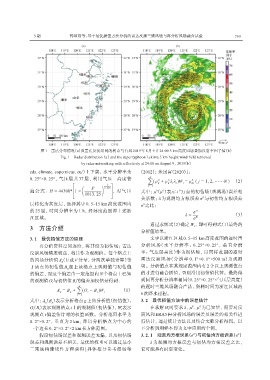
图1 雷达分布情况（a）及雷达反演组网的利奇马台风2019年8月9日24:00 5 km高度风场叠加反射率因子值（b）
Fig. 1 Radar distribution （a） and the super typhoon Lekima 5 km height wind field retrieved
by radar networking with reflectivity at 24:00 on August 9， 2019（b）
cds. climate. copernicus. eu/）上下载， 水平分辨率为 （2012）； 朱国富（2020）］：
N
0. 25°×0. 25°， 气压层共 37 层， 利用气压—高度普 ∑ ( μ ij + μ ij λ i λ j )W i = μ jg ( j = 1，2，……N ) （2）
B
O
B
1
é ê ê P 5. 256 ú ú ) ù ú ú i = 1
ê
遍公式： H = 44300*ê1 - ú ú， 对气压 式中： μ（μ ）表示 i 与 j 点的初估场（观测场）误差相
O
B
ê ê ( 1013. 25
ë û 关系数； λ 为观测均方根误差 σ 与初估均方根误差
O
层转化为高度层， 选择其中 0. 5~15 km 高度范围内 σ 之比：
B
的 25 层， 时间分辨率为 1 h， 经纬度范围即上述浙 σ O
江区域。 λ = σ B （3）
通过求解式（2）确定 W i ， 即可得到式（1）最终的
3 方法介绍
分析值结果。
3. 1 最优插值方法的原理 文中以浙江区域 0. 5~15 km 高度范围的逐时再
再分析资料空间连续， 将其设为初估场； 雷达 分析风场（水平分辨率： 0. 25°×0. 25°， 垂直分辨
反演风场精度较高， 将其作为观测值。每个格点上 率： 气压层高度）作为初估场， 以同样范围的逐时
的风场分析值 A（U 或 V 分量， 分两次单独计算）等 雷达反演风场（分辨率 0. 1°×0. 1°×500 m）为观测
g
于该点的初估值 B 加上该格点上观测值与初估值 场。分析值点在其规定范围内有 2个以上观测值点
g
的偏差， 而这个偏差由一定范围内 N 个格点上已知 的才进行融合插值， 否则沿用初估值代替。最终得
的观测值O 与初估值B 的偏差加权估计得到： 到同再分析分辨率相同（0. 25°×0. 25°×气压层高度）
i
i
N 的逐时三维风场融合产品， 资料时间为浙江区域的
（1）
A g = B g + ∑ (O i - B i )W i
i = 1 6次降水过程。
式中： A（B）表示分析格点 g上的分析值（初估值）， 3. 2 最优插值方法中的误差估计
g
g
O（B）表示观测格点 i上的观测值（初估值）， W 表示 在求解 W 时要求 λ、 μ 、 μ 为已知量， 需要对反
B
O
i
i
i
i
观测点 i 偏差估计时的权重函数。分析范围水平为 演风和 ERA5再分析风场的误差及误差的相关性进
0. 2°×0. 2°， 垂直为 2 km， 即以分析格点为中心的 行估计， 通过统计方法以及结合文献分析得到。以
一个边长0. 2°×0. 2°×2 km长方体范围。 下分析所用样本即为文中应用的个例。
O
B
假设初估场误差和观测误差无偏， 以及初估场 3. 2. 1 观测均方根误差（σ ）与初估均方根误差（σ）
误差和观测误差不相关， 最优的权重可以通过最小 λ 为观测均方根误差与初估均方根误差之比，
二乘法构建线性方程获得［具体推导参考潘旸等 它可能具有时空变化。