Page 150 - 《高原气象》2025年第3期

高 原 气 象 44 卷
708
-1 -3 为二氧 表1 不同高度不同稳定条件的可用湍流数据数量
J·kg ）， ρ v 为水汽密度（单位： kg·m ）； ρ CO 2
-3
化碳密度（单位： kg·m ）。 Table 1 The number of available segments at different
levels and under different stable conditions
根 据 Li and Bou-Zeid （2011）以 及 Wang et al
（2014）的研究， 利用以下标准对数据进一步筛选， 高度 不稳定 中性 稳定
/m （-10<ζ<-0. 05） （-0. 05<ζ<0. 05） （0. 05<ζ<10）
选择符合标准的数据： （1）湍流强度必须小于 0. 5
20 221 50 201
才能满足泰勒冻结假设。（2）动量和标量通量应大
38 195 12 131
-2
-1
于阈值： u * > 0. 01 m·s ， | H | > 10 W·m ， | L v E | >
56 146 3 104
10 W·m 。剔除异常大的湍流通量： 感热通量和潜
-2
-2
热通量应在-200~400 W·m 的范围内。 序 列 中 的 湍 流 结 构（Willmarth and Lu， 1972； Lu
经质量控制和标准筛选后， 再根据不同稳定条 and Willmarth， 1973）， 已在不同植被冠层和不同边
件筛选出可用的湍流数据。如表1。 界层中得到应用。将数据采样到 4 个不同的象限，
表 1 列出了可用湍流数据数量， 随着高度的增 如图 2， 由笛卡尔轴定义的 4 个象限用于表示四种
加， 可用湍流数据量均在下降， 可能与随着高度增 湍流传输模式：
加， 湍流运动受大尺度湍涡影响增大有关。 象限 1（Q1）： u' > 0，w' > 0 外向相互作用， a' >
2. 3 方法介绍 0， w' > 0喷射；
2. 3. 1 象限分析 象限 2（Q2）： u' < 0， w' > 0 喷射， a' < 0， w' > 0
象限分析是一种条件采样技术， 用于识别时间 外向相互作用；

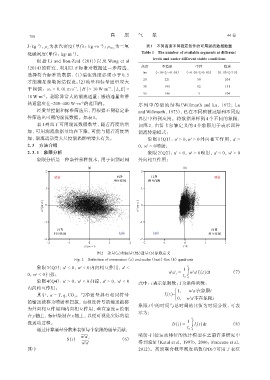
图2 动量（a）和标量（热）通量（b）象限定义
Fig. 2 Definition of momentum （a） and scalar （heat） flux （b） quadrants
象限 3（Q3）： u' < 0， w' < 0 内向相互作用， a' < - ----- 1 t a
0， w' < 0扫掠； w'a' i = ∫ w' a'I i(t) dt （7）
t a 0
象限 4（Q4）： u' > 0， w' < 0 扫掠， a' > 0， w' < 0 式中： i表示象限数； I为条件函数：
内向相互作用；
ì1， w'a'在象限i
其中， a = T，q，CO 2 。与净通量具有相同符号 I i(t)= í
î 0， w'a'不在象限i
的输送被称为喷射和扫掠， 而相反符号的输送被称
象限 i 中的时间与总时间的比值为时间分数， 可表
为外向相互作用和内向相互作用， 垂直速度 w 绘制
示为：
在 y轴上， 标量绘制在 x轴上， 以便可视化实际的湍
t a
流运动过程。 D(i) = 1 ∫ I i(t) dt （8）
通过计算通量分数来表征每个象限的通量贡献： t a 0
- ----- 喷射-扫掠运动特征的统计模型在之前许多研究中
S(i) = w'a' i （6）
- -----
w'a' 得到验证（Katul et al， 1997b， 2006； Francone et al，
其中 2012）。高斯联合概率密度函数（PDF）可用于表征