Page 150 - 《爆炸与冲击》2026年第01期

第 46 卷 李军润，等： RC箱型结构内爆炸载荷特性和动力行为分析 第 1 期

响，结构表面其余位置的冲量载荷通过线性插值确定，可能导致冲量增强因子的计算偏差。进一步拟合
得到冲量增强因子与 TNT 当量和泄爆系数之间函数关系：

−0.36
η
k 1-wall = 7.85W −0.78 −0.245W TNT (18)
TNT
−0.79 −0.067W
k 1-slab = 9.75W TNT η −1.117 (19)
TNT
2
式中：k 1-wal l 为墙体冲量增强因子，k 1-sla b 为顶板冲量增强因子。式 (18)～(19) 中，R =0.99。
4 结构动力行为
为分析内爆炸作用下泄爆系数对 RC 箱型结构毁伤效应的影响，本节通过对比自由场爆炸作用下的
结构动态响应，确定不同泄爆系数下的结构毁伤增强因子。

4.1 结构中心的动力响应
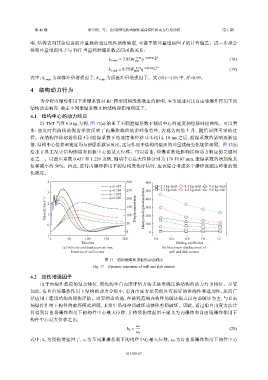
以 TNT 当量 9.0 kg 为例，图 17(a) 给出了不同泄爆系数下侧墙中心的速度和位移时程曲线。可以看
出：速度时程曲线的锯齿形状反映了内爆炸载荷的多峰值特性，表现为初始上升、随后回弹至零的过
程。在结构位移初始阶段不同泄爆系数下的速度和位移基本相同，10 ms 之后，泄爆系数的影响逐渐显
著，结构中心位移和速度均与泄爆系数呈反比，这与作用于结构内壁面的冲量载荷变化规律相同。图 17(b)
给出了各工况中结构侧墙和顶板中心的最大位移。可以看出：泄爆系数是影响结构动力响应的关键因
素之一。以泄压系数 0.457 和 1.220 为例，侧墙中心最大位移分别为 176 和 87 mm，泄爆系数的增加使其
位移减小约 50%。因此，进行内爆炸作用下的结构毁伤评估时，应该综合考虑多个爆炸波超压峰值的毁
伤效应。

4 300 600
η=0.457 2.3 kg-wall 4.5 kg-wall 9.0 kg-wall
η=0.784 250 500 2.3 kg-slab 4.5 kg-slab 9.0 kg-slab
3 η=1.002 200 400
η=2.220
Velocity/(m·s −1 ) 2 1 150 Displacement/mm Maximum displacement/mm 300

100
200
50
0 100
0 0
−1
0 50 100 150 200 0.4 0.6 0.8 1.0 1.2
Time/ms Venting coefficient
(a) Velocity and displacement-time (b) Maximum displacement of
histories of wall center wall and slab centers
图 17 结构侧墙和顶板的动态响应
Fig. 17 Dynamic responses of wall and slab centers

4.2 毁伤增强因子
由于内爆炸载荷的复杂特征，简化的单自由度评估方法无法准确反映结构的动力行为特征。尽管
如此，在自由场爆炸作用下结构的动力分析中，单自由度方法仍然具有较好的准确性和适用性，从而广
泛应用于建筑结构的毁伤评估。需要指出的是，在研究范围内构件的破坏模式以弯曲破坏为主，与自由
场爆炸作用下构件的破坏模式相同，未发生局部冲切破坏或整体剪切破坏。因此，通过单自由度方法计
算得到自由场爆炸作用下的构件中心最大位移，并将毁伤增强因子定义为内爆炸和自由场爆炸作用下
构件中心最大位移之比：
ω
k 2 = (20)
ω f
2 ω f 为自由场爆炸作用下构件中心
式中：k 为毁伤增强因子， ω 为不同泄爆系数下的构件中心最大位移，

013101-17