Page 147 - 《爆炸与冲击》2026年第01期

第 46 卷 李军润，等： RC箱型结构内爆炸载荷特性和动力行为分析 第 1 期

η=0.457

η=0.457 η=1.220
12 η=1.220 12
Impulse/(kPa·s)
Impulse/(kPa·s) 6 10 Impulse/(kPa·s) 6 9 8 7
10
Impulse/(kPa·s)
9
9
9
8
6 7 6 5
3 3
3.0 5 0 4
2.5 4 1 5
2.0 4 5 2 4 3
1.5 3 3 3
3
1.0 2 Length/m 2 2
0.5 1 Width/m 2 4 Width/m
Length/m
0 0 1
5
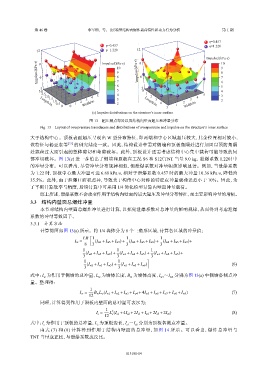
(c) Impulse distributions on the structure’s inner surface
图 13 超压测点布置以及结构内壁面超压和冲量分布
Fig. 13 Layout of overpressure transducers and distributions of overpressure and impulse on the structure’s inner surface
大于结构中心。顶板表面超压呈现出 W 型分布特征，即两端和中心区域超压较大，其余位置相对较小，
该特征与杨亚东等 [22] 的研究结论一致。因此，结构设计中需对侧墙和顶板角隅处进行加固以预防角隅
处载荷过大而引起的整体剪切和弯剪破坏。此外，顶板设计还需考虑结构中心集中载荷可能导致的局
部冲切破坏。图 13(c) 进一步给出了侧墙和顶板在工况 S6 和 S12（TNT 当量 9.0 kg、泄爆系数 1.220）中
的冲量分布。可以看出，尽管冲量分布规律相似，但泄爆系数对冲量幅值影响显著。例如，当泄爆系数
为 1.22 时，顶板中心最大冲量可达 6.68 kPa·s，相对于泄爆系数 0.457 时的最大冲量 10.36 kPa·s，降低约
35.5%。此外，由于泄爆口面积差异，导致关于构件中心对称的特征点冲量载荷误差小于 10%。因此，为
了平衡计算效率与精度，后续计算中可采用 1/4 简化模型计算内壁面冲量载荷。
综上所述，泄爆系数不会改变作用于结构内壁面的最大超压及冲量分布特征，而主要影响冲量的增幅。
3.3 结构内壁面总爆炸冲量
本节对结构内壁面总爆炸冲量进行计算，以探究泄爆系数对总冲量的影响规律，从而得到考虑泄爆
系数的冲量等效因子。
3.3.1 计算方法
计算简图如图 13(a) 所示。将 1/4 墙体分为 8 个三角形区域，计算各区域的冲量值：
ï
LB 1 1 1
I w = (I w4 + I w5 + I w7 )+ (I w8 + I w5 + I w9 )+ (I w8 + I w5 + I w7 )+
8 3 3 3
1 1 1
(I w6 + I w5 + I w9 )+ (I w1 + I w4 + I w5 )+ (I w1 + I w2 + I w5 )+
3 3 3
ò
1 1
(I w2 + I w3 + I w5 )+ (I w3 + I w5 + I w6 ) (6)
3 3
式中：I 为作用于侧墙的总冲量，L 为墙体长度，B 为墙体高度，I ～I 分别为图 13(a) 中侧墙各测点冲
w
w
8
w
w
w1
量。整理得：
1
I w = B w L w (I w1 + I w2 + I w3 + I w4 +4I w5 + I w6 + I w7 + I w8 + I w9 ) (7)
12
同理，计算得到作用于顶板内壁面的总冲量可表示为：
1 2
I s = L (I s1 +4I s2 +2I s3 + I s4 +2I s5 +2I s6 ) (8)
s
12
式中：I 为作用于顶板的总冲量，L 为顶板边长，I ～I 分别为顶板各测点冲量。
s
6
s
s1
s
由式 (7) 和 (8) 计算得到作用于结构内壁面的总冲量，如图 14 所示。可以看出，爆炸总冲量与
TNT 当量成正比，与泄爆系数成反比。
013101-14