Page 148 - 《爆炸与冲击》2026年第01期

第 46 卷 李军润，等： RC箱型结构内爆炸载荷特性和动力行为分析 第 1 期

250
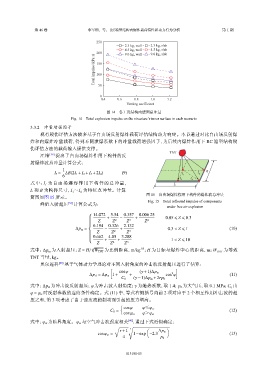
2.3 kg, wall 2.3 kg, slab
4.5 kg, wall 4.5 kg, slab
200 9.0 kg, wall 9.0 kg, slab
Total impulse/(kPa·s) 150

100

50

0
0.4 0.6 0.8 1.0 1.2
Venting coefficient
图 14 各工况结构内壁面总冲量
Fig. 14 Total explosion impulse on the structure’s inner surface in each scenario

3.3.2 冲量增强因子
现有毁伤评估方法较多基于自由场反射爆炸载荷评估结构动力响应。本节通过对比自由场反射爆
炸和内爆炸冲量载荷，得到不同泄爆系数下的冲量载荷增强因子，为后续内爆炸作用下 RC 箱型结构毁

伤评估方法的载荷输入提供支撑。
TNT
汪维 [38] 提出了自由场爆炸作用下构件的反
射爆炸波总冲量计算公式：
1 B
I f = LB(2I 1 + I 2 + I 3 +2I 4 ) (9) I 1 I 2
6
I 3 I 4
式 中 ： I f 为 自 由 场 爆 炸 作 用 下 构 件 的 总 冲 量 ， L
4
L 和 B 为构件尺寸，I ～I 为特征点冲量。计算
1
图 15 自由场爆炸作用下构件的爆炸波总冲量
简图如图 15 所示。
Fig. 15 Total reflected impulse of components
峰值入射超压 [39] 计算公式为：
under free air explosion

14.072 5.54 0.357 0.006 25
 + − + 0.05 ⩽ Z ⩽ 0.3

 Z Z 2 Z 3 Z 4


 6.194 0.326 2.132
∆p m = − + 0.3 < Z ⩽ 1 (10)
 Z Z 2 Z 3


 0.662 4.05 3.288

 + + 1 < Z ⩽ 10
Z Z 2 Z 3
√
1/3
Z = H/ W TNT 为比例距离，m/kg ；H 为目标与爆炸中心的距离，m；W T 为等效
3
式中： ∆p m 为入射超压； TN
TNT 当量，kg。
奥尔连科 [40] 基于气体动力学理论对不同入射角度的冲击波反射超压进行了估算：
ï ò
cosφ (γ +1)∆p m
2
∆p rf = ∆p m 1+ + cos φ (11)
C 0 (γ −1)∆p m +2rp 0
γ 为绝热系数，取 p 0 为大气压，取 0.1 MPa；C 由
0
式中： ∆p rf 为冲击波反射超压； φ 为冲击波入射角度； 1.4；
φ = φ cr 时反射参数的连续条件确定。式 (11) 中，等式右侧括号内前 2 项对应于 2 个相互作用冲击波的超
压之和，第 3 项考虑了由于速度流的制动而引起的压力增高。
ß
cosφ φ≤φ cr
C 0 = (12)
cosφ cr φ＞φ cr
φ cr 与空气冲击波强度相关 [40] ，通过下式近似确定：
式中： φ cr 为临界角度。

… 3 Å ã
r +1 ∆p m
cosφ cr = 1−exp −2.3 (13)
4 p 0
013101-15