Page 108 - 《爆炸与冲击》2026年第01期

第 46 卷 陈 丁，等： 非药式水下爆炸冲击波加载的PD-SPH建模与分析 第 1 期

指数衰减，冲击波在衰减过程中出现了一定程度的波动。这是由于冲击波加载装置中的环境并非无限
自由水域，冲击波到达管壁会产生反射。图 5(b) 展示了靶板中心处初始压力峰值随飞片速度的变化，该
处的压力波初始峰值与飞片的速度呈线性关系，且模拟结果与实验结果吻合良好。这说明，本数值模型
具有良好的压力预测能力，适用于求解水下爆炸冲击波加载问题。
整个算法基于文献 [20, 25, 31]，在 SParSim
表 2 模拟时长 0.6 ms 的不同 CPU/GPU 下的计算时间
的 GPU 并行框架 [34] 内，扩展了 PD-SPH 算法，并
Table 2 Computation time on different CPU/GPU
实现了多 GPU 并行。如表 2 所示，在 500 万粒子
with a simulation duration of 0.6 ms
规模的计算量下，能够实现 69 min 的响应速度。
CPU/GPU数量 配置 计算耗时/min 加速比
以 RTX3090 作为参考点，相较于单卡 RTX3090
1 AMD EPYC 9654(96核) 624 0.59
这一性能基准，96 核 CPU 的 MPI 并行计算速度
2 RTX3090 371 1.00
仅达到其 59%。主要原因在于 MPI 多核并行随
3 4卡RTX3090 152 2.44
着并行核数的上升，单线程计算的负载降低（单
4 4卡RTX4090 69 5.38
个线程的粒子数降低至 5.2 万粒子），与邻近线

程的通讯负载增加。4 卡 RTX3090 相比单卡 RTX3090 还依然能够保证 2.44 的加速比，并行效率保持为
61%。随着硬件的更新，4 卡 RTX4090 的计算速度为 4 卡 RTX3090 的 2.2 倍。
4.4 飞片冲击速度的影响
为模拟靶板的变形毁伤过程，设置其厚度为 2.5 mm，设定为 Johnson-Cook 材料模型，具体参数见表 1。
靶体结构离散间距为 0.5 mm，其余结构离散间距为 1 mm，共离散 7 607 229 个粒子。
为作比较，以非流固耦合 PD 模型作为参考，即假设与流体接触的板以均匀初速度施加初始条件，随
后的变形和破坏情况通过不考虑流体的固体 PD 模拟确定。根据 Taylor 提出的公式 [2, 4] ，假设压力波以

p = p 0 e −t/θ 的衰减形式作用在薄板上，并将压力冲量一部分转化为靶板动能，另一部分因流固耦合效应耗
ψ
散。根据流固耦合效应的影响，假设爆炸波荷载作用在靶板上，使得其获取均匀初始速度 v 0 ，引入参数
解耦流固耦合效应，具体公式为：
2p 0 θζ
v 0 = , ζ = ψ ψ/(1−ψ) (19)
m t
ψ = ρ w c w θ/m t 为 Taylor 流固耦合作
式中：θ 为指数衰减的时间常数； ζ 为总动量与传递到薄板的动量之比；
用 参 数 ， m t 为 靶 体 的 面 密 度 ， ρ w 和 c w 分 别 为 水 的 密 度 和 声 速 。 根 据 文 献 [ 2 9 ] 中 提 供 的 飞 片 速 度

p 0 = 68.27 MPa ，衰减时间常数为 43.88 μs，可知其靶体初始速度为 70.6 m/s。
140.24 m/s，对应的峰值压力
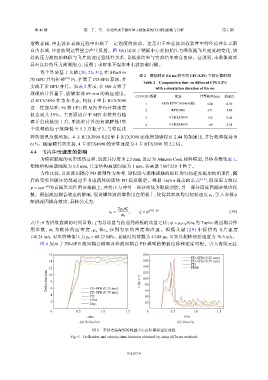
图 6 展示了 PD-SPH 流固耦合模型及非流固耦合 PD 模型的靶板位移和速度时程。引入有限元法

16 180
PD-SPH (0.25 mm)
14 160 PD-SPH (0.50 mm)
PD
140
12 120 FEM
Deflection/mm 10 8 v/(m·s −1 ) 100
80
PD-SPH (0.50 mm)
4 6 PD-SPH (0.25 mm) 60
PD
40
FEM
2 20
Exp.
0 0.5 1.0 1.5 0 0.5 1.0 1.5
t/ms t/ms
(a) Deflection (b) Velocity
图 6 不同方法得到的圆盘中心点位移和速度曲线
Fig. 6 Deflection and velocity-time histories obtained by using different methods

011107-8