Page 64 - 《爆炸与冲击》2025年第12期

第 45 卷 陈飞翔，等： 温压炸药隧道内爆炸结构约束对冲击波及爆炸火团的影响规律 第 12 期

明沿隧道轴线的距离对隧道内冲击波超压峰值分布的影响。经以上分析可知，L ＜D/3 时，隧道内冲击
e
波超压峰值分布会出现一定程度的差异；L ＞D/3 时，冲击波超压峰值分布几乎不发生变化。
e
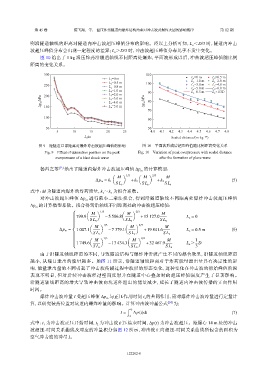
图 10 给出了 1 kg 温压炸药沿隧道轴线不同距离处爆炸，平面波形成以后，冲击波超压峰值随比例
距离的变化关系。

300 110 L e =0 m L e =0.5 m
L e =0 m L e =1.0 m L e =2.0 m
L e =0.5 m 100
250 L e =3.0 m L e =4.0 m
L e =0.8 m L e =5.0 m L e =0.0 m
L e =1.0 m 90 L e =0.5 m L e >1/3D
L e =2.0 m
200
Δp m /kPa L e =4.0 m Δp m /kPa 80
L e =3.0 m
L e =5.0 m
150
70
100 60
50 50
5 10 15 20 25 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8
L s /m Scaled distance/(m·kg −1/3 )
图 9 距隧道口部距离对爆炸冲击波超压峰值的影响 图 10 平面波形成后超压峰值随比例距离变化关系
Fig. 9 Effect of detonation position on the peak Fig. 10 Variation of peak overpressure with scaled distance
overpressure of a blast shock wave after the formation of plane wave

杨科之等 [23] 给出了隧道内爆炸冲击波超压峰值 Δp 的计算模型：
m
Å ã 1/3 Å ã 2/3
M M M
∆p m = k 1 +k 2 +k 3 (5)
S L s S L s S L s
式中：M 为隧道内爆炸的炸药质量，k ～k 为拟合系数。
3
1
对冲击波超压峰值 Δp 进行最小二乘法拟合，得到沿隧道轴线不同距离处爆炸冲击波超压峰值
m
Δp 的计算模型系数。拟合得到沿轴线不同距离处的冲击波超压峰值：
m

Å ã 1/3 Å ã 2/3
M M M

799.9 −5 586.8 +15 127.0 L e = 0


 S L s S L s S L s


 Å ã 1/3 Å ã 2/3
 M M M
∆p m = 1 007.1 −7 379.1 +19 841.6 L e = 0.5 m (6)

 S L s S L s S L s


 Å ã 1/3 Å ã 2/3
 M M M 1

1 749.6 −13 434.3 +32 467.9 L e ＞ D

S L s S L s S L s 3
由于沿隧道轴线距离的不同，导致隧道结构与爆炸冲击波产生不同的耦合效果，沿隧道轴线距离
越小，从端口泄出的能量越多。如图 11 所示，沿隧道轴线距离对于炸药能量泄出量具有决定性的影
响，能量泄出量的不同引起了冲击波传播过程中波形的形态变化，这种变化在冲击波的初始峰值阶段
表现不明显，但对后续冲击波经过壁面反射并在隧道中心叠加时的超压峰值强度产生了显著影响。
沿隧道轴线距离的增大导致冲击波向坑道外泄出的能量减少，延长了隧道内冲击波传播的正向作用
时间。
爆炸冲击波冲量 I 受超压峰值 Δp 与正压作用时间 t 的共同作用，需对爆炸冲击波冲量进行定量计
m
+
算，以研究装药位置对坑道内爆炸冲量的影响。计算冲击波冲量公式 [24] 为：
w
t 2
I = ∆p(t)dt (7)
t 1
式中：t 为冲击波正压开始时间，t 为冲击波正压结束时间，Δp(t) 为冲击波超压。距爆心 14 m 处的冲击
1
2
波超压-时间关系曲线及对应的冲量积分如图 12 所示，冲击波正向超压-时间关系曲线所包含的面积为
空气冲击波的冲量 I。
122202-8