Page 152 - 《爆炸与冲击》2025年第6期

第 45 卷 陶 明，等： 不同倾角充填节理对岩石爆破块度的影响 第 6 期

ï ò ï ò
v R p v T p
 −1 −1
 = −B Av I p (i) + B C

v R s v T s
(i) (i)
ï ò ï ò ï ò (3)
 v T p −1 −1 v R p −1 v T p
 = GD v I p (i) +G E +G F

(i+1) (i) (i)
v T s v R s v T s
ï ò ï ò
z p cos2θ T z p cos2θ T −z s sin2θ T
A = , B = ,
z p sin2θ T tanθ T /tanθ I −z p sin2θ T tanθ T /tanθ I −z s cos2θ T
ï ò ï ò ï ò
z p cos2θ T −z s sin2θ T k n ∆tcosθ I −k n ∆tcosθ I k n ∆tsinθ T
C = , D = , E = ,
−z p sin2θ T tanθ T /tanθ I −z s cos2θ T k s ∆tsinθ I k s ∆tsinθ I k s ∆tcosθ T
 
z p cos2θ T −k n ∆tcosθ I z s sin2θ T ï ò
z p cos2θ T z s sin2θ T
F =  z p sin2θ T tanθ T /tanθ I k s ∆tsinθ I  ,G =
z p sin2θ T tanθ T /tanθ I −z s cos2θ T
k s ∆tsinθ I z s cos2θ T

式中：下标 T 和 R 分别表示透射和反射，i 表示
迭代次数；v 为质点振动速度；z 为材料中的阻
抗，z= ρc，c 为材料中的波速；k 和 n k 分别为法向
s
θ T 分别为入射角和透射角 σ i σ n
和切向节理刚度， θ I 和
sinθ T /sinθ I = c s /c p 。
度，满足
τ
对于柱面波的入射，角度的变化实际上体
现在波阵面到节理的距离上，也即受到图 21 中
的 r 和 0 h 的变化控制，因此定义 h/r 作为一个无
0
图 22 节理面上的应力分量
量纲的量来表征入射角度，本文中的节理倾角可 Fig. 22 Stress component on the joint plane
以表示为 arctan(r /h)，当 h/r =1 时，对应的角度
0
0
为 45°，随着 h/r 的增大，入射角度趋近于 0°。此外定义反射系数 R 为反射波最大质点速度和入射波最
0
大质点速度的比值：
R = max|v R |/max|v I | (4)
由于爆破过程中，P 波和 S 波都对试样的破碎有贡献，进一步，定义：
»
2
R total = R +R 2 s (5)
p

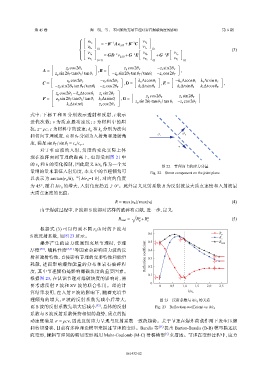
根据式 (3) 可以得到不同 r /h 0 时的 P 波与
S 波反射系数，如图 23 所示。 0.6 R p
R s
爆炸产生的应力波遇到充填节理时，节理 0.5 R total
厚度 [50] 、填料性质 [8,51] 等因素会影响应力波的反 0.4
射和透射特性，直接影响节理的变形特性和能量 Reflection coefficient 0.3
耗散，进而影响爆炸能量的分布和岩石破碎程 0.2
度，其中节理倾角是影响爆破块度的重要因素。
0.1
根据图 23，在认识节理对爆破块度的影响时，需
0
要考虑反射 P 波和 SV 波的联合作用。理论计 0 0.5 1.0 1.5 2.0 2.5
算结果表明，在入射 P 波的影响下，随着充填节 h/r 0
理倾角的增大，P 波的反射系数先减小后增大， 图 23 反射系数与 h/r 0 的关系
而 S 波的反射系数先增大后减小 [52] ，总体的反射 Fig. 23 Reflection coefficient vs. h/r 0
系数与 S 波反射系数保持相似的趋势，质点的振
动速度满足 σ = ρcv，因此反射应力呈现与反射系数一致的趋势。关于节理在爆炸荷载作用下发生压缩
和剪切滑移，目前有多种理论模型来描述节理的变形。Bandis 等 [53] 提出 Barton-Bandis (B-B) 模型描述法
向变形，倾斜节理间的剪切变形则用 Mohr-Coulomb (M-C) 滑移模型 [5] 来描述。节理在变形过程中，应力

061432-12