Page 141 - 《爆炸与冲击》2023年第2期

第 43 卷 陈源捷，等： 基于ESGA遗传算法的水射流自驱旋转喷头优化设计 第 2 期

从上述冲击扫掠轨迹线对比图中还可以发现，喷头布局对轨迹线的疏密程度有一定影响，显然优化
布局方案下的轨迹线在路径垂直方向上的分布更加均匀，而原布局方案的轨迹线为两侧稀、中间密。因
此，采用 ESGA 算法优化的布局方案能够满足在约束条件的前提下，有效提高旋转射流喷头在冲击扫掠
时的轨迹均匀度。
基于图 12 的轨迹分析发现，稳定区域内，其纵向冲击时间分布趋势基本相同。为了更加直观地体
现出旋转喷头在横向移动时，喷嘴在纵向不同位置的冲击时间对比情况，在图 12 中冲击扫掠轨迹稳定
区域内（横向距离 100～150 mm）的任一横坐标位置下，均匀地在纵向实际扫掠范围，即纵向（−50.1 mm，
50.1 mm）范围内，取 400 个观测点。采用原喷头布局方案在扫掠宽度范围内，各喷嘴和全部喷嘴的累计
冲击时间分布如图 13（a）所示，横坐标为观测点的扫掠范围，纵坐标为观测点的扫掠冲击时间。可以发
现，原布局方案下的扫掠冲击时间分布两极分化现象严重，在扫掠区域（−30 mm，−20 mm）和（20 mm，

30 mm）内，其累计扫掠时间相对较长，最大扫掠累计时间约 17 ms，会导致局部过喷现象，浪费射流能量，
甚至还可能损伤钢板基材。在扫掠区域（−50 mm，−44 mm）、（46 mm，50 mm）、（−38 mm，−36 mm）、
（36 mm，38 mm）内，其累计扫掠时间相对较短，最大扫掠累计时间不超过 10 ms，在兼顾整体均速平移的
情况下，两侧极有可能出现局部漏喷的情况，使得冲击船壁锈层时留下明显的“剥离环”。
20

20 Nozzle 1 Nozzle 1 Nozzle 5
Nozzle 2
Nozzle 6
Nozzle 2
Nozzle 3 16 Nozzle 3 Cumulative sum
Nozzle 4
Nozzle 4
Impinging duration/ms 10 Cumulative sum Impinging duration/ms 12 8
15
Nozzle 5
Nozzle 6

0 5 4 0
−60 −40 −20 0 20 40 60 −60 −40 −20 0 20 40 60
Longitudinal distance/mm Longitudinal distance/mm
(a) Impinging time distribution of original design (b) Impinging time distribution of optimal design
100 100 1.0
80 80 0.9
Longitudinal distance/mm −20 0 Longitudinal distance/mm −20 0 0.6 Relative impinging duration
60
60
0.8
40
40
0.7
20
20
0.5
0.4
−40
0.3
−40
−60
0.1
−80 −60 0.2
−80
−100 −100 0
0 50 100 150 200 250 0 50 100 150 200 250
Traverse distance/mm Traverse distance/mm
(c) Energy distribution of original design (d) Energy distribution of optimal design
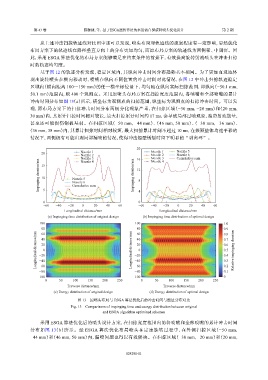
图 13 原喷头布局与 ESGA 算法优化后的冲击时间与能量分布对比
Fig. 13 Comparisons of impinging time and energy distribution between original
and ESGA algorithm optimized schemes
采用 ESGA 算法优化后的喷头设计方案，在扫掠宽度范围内的各喷嘴和全部喷嘴的累计冲击时间
分 布 如 图 13（ b） 所 示 。 经 ESGA 算 法 优 化 布 局 喷 头 在 定 速 旋 转 过 程 中 ， 在 外 侧 扫 掠 区 域 （ −50 mm，
−44 mm）和（46 mm，50 mm）内，漏喷问题也得以有效解决。在扫掠区域（−30 mm，−20 mm）和（20 mm，

024201-11