Page 308 - 《软件学报》2020年第10期

3284 Journal of Software 软件学报 Vol.31, No.10, October 2020

Fig.4 Different states of a stencil during deformation
图 4 模板变形过程中的不同状态
本文定义弯曲系数 k B ,以 k B E B 取代 E B 来控制弯曲变形能.当 k B 为 1 时,弯曲变形能较大,模型变形过程出现
−2
细微抖动.k B 为 10 时弯曲变形能较小,变形效果较为理想(如第 6 节中图 16~图 17 所示),且有效地解决了模型
弯曲变形过程中的抖动问题(如第 6 节中图 18 所示).
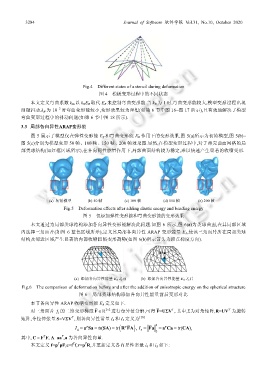
3.3 局部各向异性ARAP变形能
图 5 展示了模型仅在弹性变形能 E S 和弯曲变形能 E B 作用下的变形效果,图 5(a)所示为初始模型,图 5(b)~
图 5(e)分别为模型变形 50 帧、100 帧、150 帧、200 帧效果图.显然,在模型变形过程中,对于薄壳曲面网格的局
部类球结构(如红框区域所示),在各向同性能量作用下,局部曲面结构较为稳定,难以快速产生显著的收缩变形.

(a) 初始模型 (b) 50 帧 (c) 100 帧 (d) 150 帧 (e) 200 帧
Fig.5 Deformation effects after adding elastic energy and bending energy
图 5 仅添加弹性变形能和弯曲变形能的变形效果
本文通过为局部类球结构添加各向异性变形能解决此问题.如图 6 所示,图 6(a)为类球曲面,在其局部区域
内选择三角面片(如图 6 蓝色区域所示),定义其局部各向异性 ARAP 变形能量 E A ,使该三角面片所在局部类球
结构及邻近区域产生显著的内部收缩凹陷变形趋势(如图 6(b)所示箭头为顶点梯度方向).

(a) 添加各向异性能量 E A 之前 (b) 添加各向异性能量 E A 之后
Fig.6 The comparison of deformation before and after the addition of anisotropic energy on the spherical structure
图 6 局部类球结构添加各向异性能量前后变形对比
本节各向异性 ARAP 收缩变形能 E A 定义如下.
T
对三角面片 f j 的二维变形梯度 ∈F R 22× 进行奇异值分解,可得 =FUΣV T , 其中,Σ为对角矩阵,R=UV 为旋转
矩阵,令拉伸张量 =VS ΣV T , 则各向异性常量 I 4 和 I 5 定义为 [18]
I = 4 T = a Sa tr(SA = ( ) tr R FA ) , I = 5 2 2 = Fa T =a Ca tr(CA
),
T
T
其中, C = F T , F A=aa ,a 为各向异性向量.
T
T
T
本文定义 f=p pF,c=f f,r=p R,并重新定义各向异性常量 i 4 和 i 5 如下: