Page 278 - 《软件学报》2020年第10期

3254 Journal of Software 软件学报 Vol.31, No.10, October 2020

但是,使用复合网格的问题在于,对于不同的流体场景鲁棒性较差,而且维护不同形状网格的过程比较复
杂,同时,在计算精度上也存在不同程度的损失.

(a) 文献[36]中所用网格结构 (b) 文献[38]中所用网格结构
Fig.2 Fluid solvers using composite grid structures
图 2 流体求解的复合网格结构
1.3 降维计算方法

模型缩减法(降维)也是一类加速泊松方程的常见算法.在实现降维的过程中,浅水方程的应用较为常见.
Wang 等人 [40] 用浅水场方程代替三维 N-S 方程来模拟物体表面上的流动,而 Thurey 等人 [41] 结合了高度场和 SPH
方法,实现了卷浪花的效果和浅水区域的实时模拟.而在模型缩减方法中,Treuille 等人 [42] 在 SIGGRAPH 的论文
中引入了模型缩减法,实现了大规模的实时流体模拟.其基本思想是:将原本的高维度速度场缩减到低维度的基
函数子空间,然后在子空间上用缩减模型求解泊松方程.而 Wicke 等人 [43] 则进一步通过模块化思想对场景进行
分块计算,实现了场景的局部拼板式重组.文献[44]中,Kim 等人利用 Cubature 方法在子空间上实现了半拉格朗
日对流,在子空间上重新模拟出原数据结果.同时,人们也为流体动画的模型缩减方法提出了各种基函数,例如
Legendre 多项式 [45] 、三角函数 [46] 以及能够保持无散性的拉普拉斯特征向量 [47] .Ando 等人 [48] 则提出一个新的基
于集合降维技术来加速流体方程的计算过程.最近,针对模型缩减的数值耗散问题,Liu 等人 [49] 提出一种模型缩
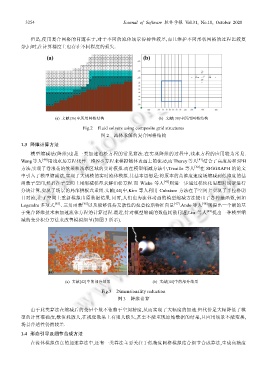
减的变分积分方法来改善模拟细节(如图 3 所示).

(a) 文献[42]中的部分结果 (b) 文献[44]中的部分结果
Fig.3 Dimensionality reduction
图 3 降维计算
由于此类算法在缩减后的变量个数不依赖于空间精度,从而实现了大幅度的加速.但代价是大幅降低了模
型的计算准确度,数值耗散大,在视觉效果上有很大缺失,甚至不能重现原始数据的结果,且应用场景不能变换,
场景普适性仍然较差.
1.4 形态引导及细节合成方法
在流体模拟仿真的加速算法中,还有一类算法主要关注于低精度网格模拟结合细节合成算法,生成高精度