Page 25 - 《真空与低温》2025年第4期

440 真空与低温 第 31 卷 第 4 期

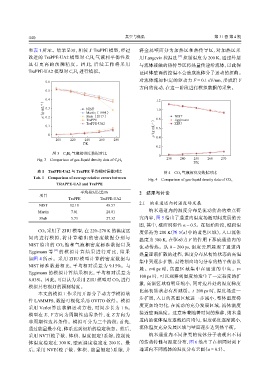
和表 1 所示。结果显示，相较于 TraPPE 模型，经过 将金属壁面分为加热区和热传导区，对加热区采
改进的 TraPPE-UA2 模型对 C 2 H 6 气液相平衡性质 用 Langevin 控温法 [15] 控制温度为 200 K，通过外层
具 有 更 高 的 预 测 精 度 。 因 此， 后 续 工 作 将 采 用 与流体接触的热传导区将热量传递给流体，以此保
TraPPE-UA2 模型对 C 2 H 6 进行模拟。 证固体壁面的控温不会造成流体分子运动的扭曲。
对流体施加恒定的驱动力 F = 0.1 eV/nm，形成沿

0.6 Y
方向的流动，在这一阶段进行模拟数据的采集。
0.5

0.4 1.2
ρ/ （ g·mL −1 ） 0.3 NIST 1.0
Martin（1998）
Shah（2017）
0.2
Eggimann
TraPPE 0.8 NIST
TraPPE-UA2 ZHU
0.1 ρ/ （ g·mL −1 ） 0.6
0
200 220 240 260 280 0.4
T/K
0.2
图 3 C 2 H 6 气液相密度数据对比
0
230 240 250 260 270
Fig. 3 Comparison of gas-liquid density data of C 2 H 6
T/K

表 1 TraPPE-UA2 与 TraPPE 平均相对误差对比 图 4 CO 2 气液相密度数据对比
Tab. 1 Comparison of average relative errors between
Fig. 4 Comparison of gas-liquid density data of CO 2
TRAPPE-UA2 and TraPPE
平均相对误差/% 2 结果与讨论
项目
TraPPE TraPPE-UA2
2.1 纳米通道内的温度场发展
NIST 12.10 48.57
纳米通道内的温度分布是流动传热的重点研
Martin 7.01 28.81
Shah 5.73 27.32 究内容，图 5 给出了通道内温度场随时间发展的云
图，其中，壁面润湿性 α = 0.5。在初始阶段，壁面温
CO 2 采用了 ZHU 模型，在 220~270 K 的温度区 度保持为 200 K（图 5（a）中的蓝色区域），入口流体
间 内 进 行 模 拟， 将 计 算 输 出 的 密 度 数 据 分 别 与 温度为 300 K，在驱动力 F 的作用下形成通道内的

NIST 给出的 CO 2 饱和气液相密度标准数据以及
流动传热。从 0～200 ps，温度云图展现了通道内
Eggimann 等 [14] 的 模 拟 计 算 结 果 进 行 对 比 ， 结 果
热量逐渐扩散的过程，温度分布从初始状态的高温
如图 4 所示。采用 ZHU 模型计算的密度数据与
集中到逐步扩散，最终朝向均匀分布的热平衡态发
NIST 标准数据相比，平均相对误差为 9.15%。与
展。t=0 ps 时，高温区域集中在通道的中央。t=
Eggimann 的模拟计算结果相比，平均相对误差为
100 ps 时，可以观察到温度场发生了一定程度的扩
6.83%。因此，可以认为采用 ZHU 模型对 CO 2 进行
散，高温区域有明显缩小，同时边界处的温度梯度
模拟具有很好的预测精度。
比起初始状态有所减缓。t=200 ps 时，温度场进一
本文的模拟工作采用开源分子动力学模拟软
步扩展，入口的高温区域进一步减小，整体温度梯
件 LAMMPS，数据可视化采用 OVITO 软件。模拟
度更加均匀化，在流动的充分发展区域，流体温度
采用 Verlet 算法求解运动方程，时间步长为 1 fs。
接近壁面温度。这意味着随着时间的推移，纳米通
模型在 X、Y 方向为周期性边界条件，在 Z 方向为
非周期性边界条件。模拟可分为三个阶段：首先， 道内的流体温度逐渐趋向均匀，温度梯度逐渐减小，
通过能量最小化，体系达到初始的稳定状态。然后， 流体温度充分发展区域与壁面逐步达到热平衡。
采用 NVT（粒子数、体积、温度恒定）系综，控制流 纳米通道内不同种类的流体分子表现出不同
体温度稳定在 300 K，壁面温度稳定在 200 K。最 的传热特性与温度分布，图 6 给出了在相同时刻下
后，采用 NVE（粒子数、体积、能量恒定）系综，并 通道内不同流体的温度分布云图（α = 0.5）。