Page 38 - 《软件学报》2025年第9期

李奕瑾 等: 基于 RISC-V VLIW 架构的混合指令调度算法 3949

为了探索 IPC 理论模型与指令规模的关系, 我们也研究了在不同的指令规模下, IPC 理论模型的准确性变化.
从表 5 中可以看出, 在调度区域内指令数≤5 时, IPC 理论模型在 CoreMark 和 AlexNet 上的准确率达到了 100%
和 99.57%. 这是因为指令数较少时, 指令依赖和资源依赖的相互干扰较少, 理论模型能够得到准确结果. 在指令数
为 6–15 之间, 准确率稍有下降, 但仍高达 97.22% (CoreMark) 和 92.68% (AlexNet). 当指令数≥16 时, 准确率持续
下降. 但是从表 5 中可以看出, 指令数≤15 的调度区域占比为 92.16% (CoreMark) 和 93.85% (AlexNet). 因此, 理论
模型在指令数≤15 时的高准确率是有意义的. 为了更为详细地看出调度区域内指令数对理论模型的准确率的影
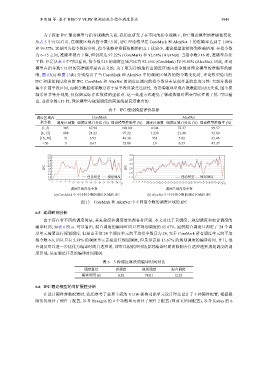
响, 图 13(a) 和图 13(b) 分别给出了当 CoreMark 和 AlexNet 中的调度区域内的指令数变化时, 理论模型给出的
IPC 和规划调度给出的 IPC. CoreMark 和 AlexNet 的调度区域内的指令数分布呈现显著的非均匀性: 大部分数据
集中在前半段区间, 而剩余数据则零散分布于后半段且缺乏连续性. 为更清晰地呈现有效数据的对比关系, 图中横
轴采用非等分刻度, 仅保留实际存在数值的坐标点. 这一处理方式避免了稀疏数据对图表可读性的干扰. 可以看
出, 当指令数≤15 时, 理论模型与规划调度的两条线是高度重合的.

表 5 IPC 理论模型评价指标

调度区域内 CoreMark AlexNet
指令数 调度区域数 调度区域百分比 (%) 理论模型准确率 (%) 调度区域数 调度区域百分比 (%) 理论模型准确率 (%)
[1, 5] 303 67.94 100.00 4 144 72.37 99.57
[6, 15] 108 24.22 97.22 1 230 21.48 92.68
[16, 50] 31 6.95 48.38 333 5.82 65.46
>50 3 0.67 75.00 19 0.33 47.37

2.8 3.2
2.6 2.8
2.4
2.2 2.4
IPC 2.0 IPC 2.0
1.8
1.6
1.4 1.6
1.2 理论模型 规划调度 1.2 理论模型 规划调度
1.0
1 3 5 7 9
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 51 53 58 65 67 76 115 157
11
17
15
13
22
33
45
69
29
25
31
135
调度区域内指令数 调度区域内指令数
(a) CoreMark 中不同指令数的调度区域的 IPC (b) AlexNet 中不同指令数的调度区域的 IPC
图 13 CoreMark 和 AlexNet 中不同指令数的调度区域的 IPC

6.5 编译时间分析
由于存在着不同的调度算法, 其复杂度和调度效果都各有区别. 本文对比了表调度、规划调度和混合调度的
编译时间, 如表 6 所示. 可以看出, 混合调度的编译时间只有规划调度的 15.67%. 虽然混合调度只判定了 24 个调
度单元需要进行规划调度, 但是由于这 24 个调度单元的平均指令数目为 26, 大于 CoreMark 所有调度单元的平均
指令数 6.4, 所以只有 5.38% 的调度单元需要进行规划调度, 但是却需要 15.67% 的规划调度的编译时间. 并且, 混
合调度可以进一步优化为编译时间自适应的, 即可以根据应用场景对编译时间的限制去自适应选择规划调度的调
度区域, 从而满足任意的编译时间限制.

表 6 3 种调度算法的编译时间对比

调度算法 表调度 规划调度 混合调度
编译时间 (s) 0.58 78.01 12.23

6.6 IPC 理论模型的可扩展性分析
在设计硬件参数配置时, 我们参考了业界主流的 VLIW 架构功能单元设计理念设计了 3 种硬件配置, 根据极
限情况设计了硬件 1 配置, 参考 Hexagon 的 4 个功能单元设计了硬件 2 配置 (即前文所用配置), 参考 Kalray 的 6