Page 37 - 《软件学报》2025年第9期
P. 37
3948 软件学报 2025 年第 36 卷第 9 期
500 500
450 426 450 422
400
400
调度区域个数 350 调度区域个数 350
300
300
250
250
200
200
150
150
100
50
50 19 1 100 22 1 1
0 0
0 1 2 0 1 2 3
(a) 理论模型与规划调度结果的 cycle 差值 (b) 理论模型与表调度结果的 cycle 差值
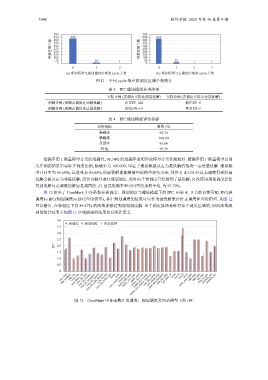
图 11 不同 cycle 数差值调度区域个数统计
表 3 IPC 理论模型分类结果
实际正例 (表调度实际达到最优解) 实际负例 (表调度实际未达最优解)
预测正例 (预测表调度达到最优解) 真正TP=422 假正FP=0
预测负例 (预测表调度未达最优解) 假负FN=19 真负TN=5
表 4 IPC 理论模型评价指标
评价指标 数值 (%)
准确率 95.74
精确率 100.00
召回率 95.69
F1值 97.79
准确率用于衡量模型分类的准确性, 95.74% 的准确率说明理论模型分类性能较好. 精确率用于衡量模型识别
为正例的结果中实际正例的比例, 精确率为 100.00% 印证了理论模型认定为最优解的情况一定是最优解. 理论模
型召回率为 95.69%, 这意味着 95.69% 的最优解都能够被理论模型定位出来, 即仅有 4.31% 经过表调度得到的最
优解会被认定为非最优解, 需要再额外进行规划调度. 此时由于表调度已经得到了最优解, 再次使用规划调度算法
得到的解与表调度的解应是相同的. F1 值是准确率和召回率的加权平均, 为 97.79%.
图 12 给出了 CoreMark 中各函数在表调度、规划调度与理论模型下的 IPC. 由第 4、5 节的内容可知, IPC(表
调度) ⩽ IPC(规划调度) ⩽ IPC(理论模型), 其中规划调度的结果可以作为最优解来评价表调度和理论模型. 从图 12
可以看出, 在表调度下有 89.47% 的函数能够达到规划调度解. 由于调度算法是针对单个调度区域的, 因此函数级
别的统计结果不如图 11 区域级别的结果更有统计意义.
4.0
表调度 规划调度 理论模型
3.5
3.0
2.5
IPC 2.0
1.5
1.0
0.5
0
图 12 CoreMark 中各函数在表调度、规划调度及理论模型下的 IPC