Page 34 - 《软件学报》2025年第8期

刘宗鑫 等: 神经网络的增量验证 3457

证接近边界的性质的性能在评估基于 SMT 的验证工具时至关重要. 为了公平比较, 我们没有启用类似 PGD [27] 的
攻击方法, 并在单进程环境中部署 DeepInc、Marabou、α, β-CROWN 和 IVAN 的实验. α, β-CROWN 是连续多年
VNN-COMP 比赛的冠军, 所以与 α, β-CROWN 的比较有更助于展示 DeepInc 在特定验证问题上的效率. 由于 α, β-
CROWN 本身不支持增量验证, 因此我们直接使用其验证修改后的网络. 而 DeepInc 与 IVAN 则先对原始网络进
行验证生成搜索树, 再利用搜索树验证修改后的网络. 此外, 我们构建的这些具有挑战性的性质将有助于对神经网
络验证工具在极其困难的性质上的性能评估的研究. 神经网络验证问题的难度不仅与神经网络的大小有关, 还与
被验证的特定性质有关. 对于大型卷积或残差网络, 如果性质远离鲁棒性边界, 验证可能很容易. 对于接近鲁棒性
边界的性质, 即使是非常小的全连接网络, 如 ACAS Xu, 也可能为当前最先进求解器带来挑战.
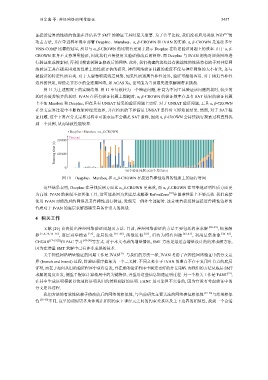
图 11 为上述配置下的实验结果. 图 11 中每根柱为一个验证问题, 柱高为不同工具验证该问题的耗时, 较少的
耗时会覆盖较多的耗时. IVAN 在所有验证问题上都超时. α, β-CROWN 的验证效率在具有 SAT 结果的验证问题
上不如 Marabou 和 DeepInc, 但在具有 UNSAT 结果的验证问题上更好. 对于 UNSAT 验证问题, 工具 α, β-CROWN
在分支定界过程中不断收紧神经元边界, 并在约束的下界满足 UNSAT 条件时立即返回结果. 然而, 对于 SAT 验
证问题, 这个下界在分支定界过程中可能永远不会满足 SAT 条件, 因此 α, β-CROWN 会持续执行搜索过程直到找
到一个反例, 从而导致性能较差.

DeepInc Marabou α, β-CROWN
Timeout
20 000
Running time (s) 10 000

0
96个验证问题 (有8个均为0 s)
图 11 DeepInc、Marabou 和 α, β-CROWN 在接近鲁棒性边界的性质上的运行时间

这些结果表明, DeepInc 在寻找反例方面比 α, β-CROWN 更高效, 而 α, β-CROWN 在可靠地证明性质方面更

为高效. IVAN 的表现不如其他工具, 这可能是因为其底层求解器 RefineZono [28] 在困难性质上不够高效. 我们直接
使用 IVAN 对修改后的网络及其鲁棒性进行验证, 发现无一例外全部超时. 这意味着我们验证接近鲁棒性边界的
性质对于 IVAN 的底层求解器确实具备非常大的挑战.

4 相关工作

文献 [29] 首次提出神经网络验证问题及方法. 目前, 神经网络验证的方法主要包括约束求解 [30−33] , 抽象解
释 [5,6,28,34−36] , 逐层穷举搜索 [37] , 全局优化 [38−40] , 函数近似 [41] , 归约为博弈问题 [42,43] , 利用星集抽象 [44−46] ,
CEGAR [17−19,22] 和 PAC 学习 [47−50] 等方式. 对于本文考虑的增量情况, SMT 方法是最适合增量设计的约束求解方法,
因为在增量 SMT 求解中已有许多成熟的技术.
关于神经网络增量验证的同期工作是 IVAN [23] . 与我们的方法一样, IVAN 考虑了在神经网络验证中的分支定
界 (branch and bound) 过程, 将验证程序抽象为一个二叉树. 不同之处在于 IVAN 的重点不在于复用叶节点的底层
证明, 而在于如何从旧的验证程序中获得启发, 并在新的验证程序中制定更好的分支策略. 而我们的方法从底层 SMT
求解的角度出发, 侧重于提取计算格局中的关键特征, 并重用这些信息加速证明过程. 另一个相关工作是 FANC [51] ,
在其中生成证明模板以快速将证明从旧的转移到新的证明. FANC 是可靠但不完备的, 因为它没有考虑验证中的
分支定界过程.
我们方法的有效性依赖于修改前后的网络的相似性, 与当前研究主要关注的网络表征相似性 [52−54] 与结果相似
性 [55−57] 不同, 这里的相似更多地体现在相同约束下神经元之间的约束关系以及上下边界的相似性, 找到一个合适