Page 314 - 《软件学报》2025年第7期

赵相福 等: BWSS: 结合可疑集合簇计算极小碰集的 Boolean 算法 3235

0.170 6 0.162 16
0.165 5 0.160 14
Minimal time/Bool time 0.155 4 Number of MHSs and HSs (×10 5 ) Minimal time/Bool time 0.154 10 Number of MHSs and HSs (×10 5 )
0.158
12
0.160
0.156
8
3
0.152
0.150
0.150
6
2
0.148
0.145
Min/Bool
MHSs
MHSs
0.140
2
HSs
HSs 1 0.146 Min/Bool 4
0.144
0.135 0 0.142 0
40 50 60 70 80 90 100 40 50 60 70 80 90 100
m m
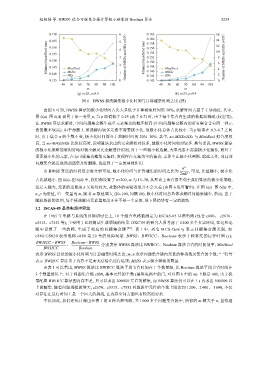
(g) n=20, p=0.4 (h) n=25, p=0.4
图 6 BWSS 算法解集极小化时间与计算碰集时间之比 (续)

由图 6 可知, BWSS 算法的极小化时间占比大多低于计算碰集时间的 30%, 求解时间占据了主导地位. 其中,
图 6(a)–图 6(d) 设置了单一变量 p, 当 p 取值低于 0.25 (高于 0.7) 时, 由于每个集合内生成的数据较稀疏 (较密集),
在 BWSS 算法求解时, 中间问题集合簇生成单元素集合的概率较高 (中间问题集合簇内的所有集合含有同一种元
素的概率较高), 由于命题 3, 候选解内较多元素不需要极小化, 故极小化总体占比较小. 当 p 取值在 0.3–0.7 之间
时, 由于集合 n 的个数不变, 极小化时间都介于求解时间的 20%–30%. 其中, no-MHSs/HSs 与 Min/Bool 拟合度较
高, 当 no-MHSs/HSs 比值较高时, 说明算法求出的冗余解相对较多, 故极小化时间相对较多. 换句话说, BWSS 算法
的极小化策略能够很好地对极小解及冗余解进行识别, 对于一些极小候选解, 大量元素不需要极小化操作, 而对于
需要极小化的元素, 在与可疑集合簇取交集时, 发现存在交集为空的集合, 立即中止极小化判断. 除此之外, 当局部
问题集合簇发现局部超集及时删除, 也起到了一定的剪枝作用.
n 2
由 BWSS 算法的时间复杂度分析可知, 极小化时间与计算碰集的时间之比为 , 可见, 比值越小, 极小化
2mk 2
占比就越小. 图 6(a)–图 6(d) 中, 我们都设置了 n=200, m 为 15–30, 从理论上来看很不利于我们算法的极小化策略,
但是 n 越大, 元素的重复度 k 又相对较大, 故整体的实验效果并不会太差 (由图 6 也可看出). 在图 6(e)–图 6(h) 中,
n, p 为定值, 单一变量为 m, 随着 m 取值增大 (20–100, 间隔 10), 极小化时间占总体求解时间越来越少. 然而, 由于
随机数据的原因, 每个候选解内元素重复度 k 并不是一个定值, 故下降趋势有一定的波动.

3.2 ISCAS-85 基准电路冲突集
在 1985 年电路与系统的国际研讨会上, 10 个组合电路被确定为 ISCAS-85 基准电路 (包含 c880、 c2670、
c5315、c7552 等), 主要用于比较测试生成领域的结果. DXC’09 的研究人员考虑了 1 400 多个真实环境, 在这些电
路中设置了一些故障, 生成了相应的问题集合簇 [20] . 表 1 中, 列名 MCS-family 表示问题集合簇类别, 如
c880:CS020 表示电路 c880 第 20 号的故障场景. BWSS、BWIICC、Boolean 表示 3 种算法的运行时间 (s);
BWIICC − BWSS Boolean− BWSS
、 分别表示 BWSS 算法比 BWIICC、Boolean 算法节省的时间效率; Min/Bool
BWIICC Boolean
表示 BWSS 算法的极小化时间与计算碰集时间之比; m, n 表示问题集合簇内元素的种类数及集合的个数; “–”符号
表示 BWIICC 算法由于内存不足而无法给出运行结果; MHSs 表示极小碰集的数量.
由表 1 可以看出, BWSS 算法比 BWIICC 算法平均节省时间在 1 个数量级, 比 Boolean 算法平均节省时间在
3 个数量级以上. 对于问题集合簇 c880, 基本元件的个数 (基准电路中的门, 对应图 6 中的 m) 上限是 400, 由于机
器配置 BWIICC 算法因内存不足, 只可以求出 200 000 左右的解集, 而 BWSS 算法仍可以在 1 s 内求出 500 000 以
上的解集. 随着问题规模的增大, c2670、c5315、c7552 问题簇中元件的个数上限达到 1 200、2 400、 3 600, 不仅
对算法在运行时间上是一个巨大的挑战, 在内存空间方面也有较高的要求.
不仅如此, 我们还统计得出在表 1 的 4 种基准电路, 共 1 000 多个问题集合簇中, 所有的 m 都大于 n, 且有超