Page 312 - 《软件学报》2025年第7期

赵相福 等: BWSS: 结合可疑集合簇计算极小碰集的 Boolean 算法 3233

25 700 10 4 7 000
BWSS
MHS-DMECV 600 6 000
20 Boolean 10 3
BWIICC 500 5 000
STACCATO
CPU time (ms) 15 MHSs 400 Number of MHSs CPU time (ms) 10 2 1 BWSS 4 000 Number of MHSs
300
3 000
10
10
Boolean
5 200 10 0 MHS-DMECV 2 000
BWIICC
100 1 000
STACCATO
MHSs
0 0 10 –1 0
0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
p p
(a) m=15 (b) m=20
10 3 4.0 10 4 35
10 2 3.5 10 3 30
3.0
10 1 2.5 10 2 25
CPU time (s) 10 –1 0 2.0 Number of MHSs (×10 4 ) CPU time (s) 10 1 0 20 Number of MHSs (×10 4 )
10
15
10
1.5
MHS-DMECV
MHS-DMECV
10 –2 BWSS 10 –1 BWSS 10
Boolean 1.0 Boolean
BWIICC BWIICC
10 –3 STACCATO 0.5 10 –2 STACCATO 5
MHSs MHSs
10 –4 0 10 –3 0
0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
p p
(c) m=25 (d) m=30
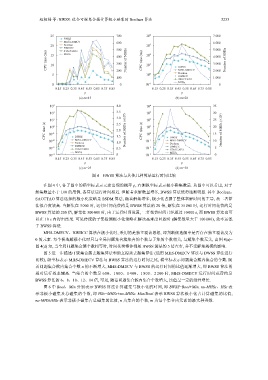
图 4 BWSS 算法与其他几种算法运行时间比较

在图 4 中, 各子图中的横坐标表示元素出现的概率 p, 右侧纵坐标表示极小碰集数量. 从图中可以看出, 对于
解集数量小于 100 的用例, 各算法运行时间相近. 但随着求解数量增多, BWSS 算法优势逐渐明显. 其中 Boolean、
SACCTAO 算法选择的极小化策略是 SSDM 算法, 随着解集增多, 极小化占据了整体求解时间的主导, 故二者算
法拟合度较高. 当解集在 3 000 时, 运行时间花费约是 BWSS 算法的 20 倍, 解集在 35 000 时, 运行时间花费约是
BWSS 算法的 200 倍, 解集在 300 000 时, 由于运行时间设置, 二者花费时间已经超过 10 000 s, 而 BWSS 算法也可
以在 10 s 内得出结果. 可见传统的子集检测极小化策略在解决高难度问题时 (解集数量大于 100 000), 效率远低
于 BWSS 算法.
MHS-DMECV、BWIICC 算法在极小化时, 采用的是独立覆盖思想, 即判断候选解中是否存在独立覆盖度为
0 的元素. 每个候选解极小化时只与全局问题集合簇集合的个数与子集的个数相关, 与解集个数无关, 由图 4(a)–
图 4(d) 知, 当全局问题集合簇个数相等时, 时间花费整体都是 BWSS 算法的 5 倍左右, 并不受解集规模的影响.
图 5 进一步描述可疑集合簇去超集算法和独立覆盖去超集算法 (选用 MHS-DMECV 算法与 BWSS 算法进行
比较), 纵坐标表示 MHS-DMECV 算法与 BWSS 算法的运行时间之比, 横坐标表示问题集合簇内集合的个数. 随
着问题集合簇内集合个数 n 的不断增大, MHS-DMECV 与 BWSS 的运行时间的比值逐渐增大, 即 BWSS 算法的
相对运行效率越高. 当集合的个数是 600、1 000、1 400、1 800、2 200 时, MHS-DMECV 运行时间花费约是
BWSS 算法的 6、8、10、12、14 倍, 可见, 随着问题集合簇内集合个数增大, 比值呈一定的线性增长.
图 6 中 Bool、Min 分别表示 BWSS 算法计算碰集与极小化的时间, 即 BWSS=Bool+Min. no-MHSs、HSs 表
示非极小碰集及总碰集的个数, 即 HSs=MHSs+no-MHSs. Min/Bool 表示 BWSS 算法极小化占计算碰集的比值,
no-MHSs/HSs 表示非极小碰集占总碰集的比值, n 为集合的个数, m 为每个集合内元素的最大种类数.