Page 22 - 《软件学报》2025年第7期

王树兰 等: eDPRF: 高效的差分隐私随机森林训练算法 2943

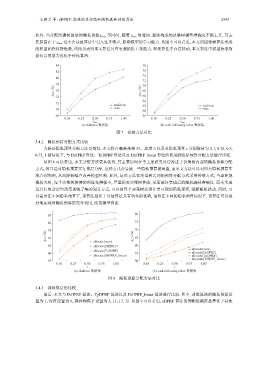
ε tree 的增加, 算法构成的决策树模型准确度不断上升, 其主
此外, 当分配给建树算法的隐私预算 ε tree 不同时, 随着
ε tree 过小会导致算法中引入过多噪声, 影响模型的学习能力. 从图中可以看出, 本文所提建树算法形成
要原因在于
的模型始终保持优势, 该结果表明本文算法具有更强的抗干扰能力. 即使算法中存在扰动, 本文算法中模型获取数
据信息的能力也优于传统算法.

84 78
82 76
74
80
72
78 70
Acc (%) 76 Acc (%) 68
74 66
64
72
tradition 62 tradition
ours
70 ours
60
68 58
0.10 0.25 0.50 0.75 1.00 0.10 0.25 0.50 0.75 1.00
ε tree ε tree
(a) diabetes 数据集 (b) wall-following robot 数据集
图 7 建树方法对比

5.4.2 隐私预算分配方式比较
为验证隐私预算分配方法有效性, 本文将在森林规模 35、深度 6 以及总隐私预算 ε 分别取值为 0.1, 0.25, 0.5,
0.75, 1 的情况下, 与 DiffPRF 算法、TpDPRF 算法以及 DiffPRF_linear 算法所使用的隐私预算分配方法进行比较.
从图 8 可以看出, 本文分配方法更具优势, 其主要原因在于上述研究尽管改进了决策树内部的隐私预算分配
方式, 但只是对隐私预算实行按层分配. 这种方式会导致一些隐私预算被闲置, 而本文方法可以对所有隐私预算实
现合理利用, 从而降低噪声改善模型性能. 此外, 这些方法在决策树之间的预算分配方式采用传统方式, 当森林规
模较大时, 每个决策树获得的预算变得极小, 严重损害决策树性能, 从而破坏集成后的随机森林准确度. 而本文通
过并行组合定理改变训练子集的划分方式, 可以使每个决策树获得非常可观的隐私预算, 缓解随机扰动. 同时, 可
以看出在不同隐私预算下, 该算法相比于其他算法具有明显的优势, 说明在不同的隐私预算情况下, 该算法可以很
好地实现对隐私预算的充分利用, 改善模型性能.

85 80
80 75

75 70
Acc (%) 70 Acc (%) 65

allocate(DiffPRF)
65 allocate(ours) 60
allocate(ours)
allocate(TpDPRF)
60 55 allocate(DiffPRF)
allocate(DiffPRF_linear) allocate(TpDPRF)
allocate(DiffPRF_linear)
55 50
0.10 0.25 0.50 0.75 1.00 0.10 0.25 0.50 0.75 1.00
ε ε
(a) diabetes 数据集 (b) wall-following robot 数据集
图 8 隐私预算分配方法对比

5.4.3 训练算法的比较
最后, 本文与 DiffPRF 算法、TpDPRF 算法以及 DiffPRF_linear 算法进行比较. 其中, 训练算法的隐私预算设
置为 1, 深度设置为 6, 森林规模 T 设置为 5, 11, 17, 35. 从图 9 可以看出, eDPRF 算法的预测准确度显著优于其他