Page 169 - 《软件学报》2025年第5期

张文跃 等: 基于高斯混合多层自编码器的情感漂移检测模型 2069

为漂移指标用 p 表示, p 值越大说明漂移越显著.
前面提到的 HVAE 模型使用 ADD 算法 (累积分布差), 该算法用到了两种分布的均值和变量. ADD 中的漂移
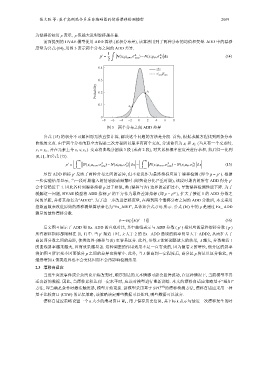
度量为公式 (14), 用图 3 表示两个分布之间的 ADD 差异.

∫
1
2
′
p = N(x;µ new ,σ 2 new )− N(x;µ θ ,σ )dx (14)
θ
2

0.4
z′|z
z′ new |S new
0.3
Probability 0.2 x 2
0.1
x 1
0
−8 −6 −4 −2 0 2 4 6 8
图 3 两个分布之间 ADD 差异

公式 (15) 的积分不可解因而无法直接计算, 解决这个问题的方法是分段. 首先, 根据求解方程找到两条分布

曲线的交点. 由于两个分布的联立方程是二次方程所以最多有两个交点, 分别命名为 x 1 和 x 2 (当只有一个交点时,
x 1 = x 2 , 并在元素上令 x 1 ⩽ x 2 ). 交点将曲线分割成 3 段 (或者 2 段), 对其累积概率密度差进行求和, 然后归一化到
[0,1] , 如公式 (15).

∫ ∫
x 1 [ ] x 2 [ ]
′ 2 2 2 2
θ
θ
p = N(x;µ new ,σ )− N(x;µ θ ,σ ) dx − N(x;µ new ,σ )− N(x;µ θ ,σ ) dx (15)
new new
−∞ −∞
尽管 ADD 指标 p 反映了两种分布之间的差异, 但不建议作为最终指标应用于漂移检测 (即令 p = p ). 根据
′
′
一些实验结果显示, 当一段时期输入的情感波动频繁时 (即舆论分化严重时期), 该段时期内的所有 ADD 得分 p ′
会非常趋近于 1. 因此各时刻漂移指标 p 过于相似, 类 (漂移与否) 边界的差距过小, 导致漂移检测性能下降. 为了
缓解这一问题, HVAE 模型将 ADD 指标 p 的平方作为最终差异指标 (即 p = p ′2 ), 扩大了接近 1 的 ADD 分数之
′
间的差距, 并将其命名为“ADD2”. 为了进一步改进漂移度量, 在得到两个情感分布之间的 ADD 分数后, 本文采用
指数函数来改进原始的漂移测量算法命名为“Ex_ADD”, 具体如公式 (16) 所示. 公式 (16) 中的 p 是通过 Ex_ ADD
测量的最终漂移分数.

[ ]
p = exp λ(p −1) (16)
′
后文图 4 展示了 ADD 和 Ex_ADD 的直观对比, 其中曲线表示与 ADD 分数 ( p ) 相对应的最终漂移分数 ( p )
′
所有漂移指标都限制在 [0, 1] 中. 当 p 接近 1 时, λ 大于 2 的 Ex_ ADD 曲线的斜率明显大于 ADD2, 从而扩大了
′
高区间分数之间的差距, 使类边界 (漂移与否) 更容易区分. 此外, 参数 λ 能够调整放大的效果, λ 越大, 分数接近 1
λ 的增长, 低分区的斜率
的曲线斜率越来越大, 因而效果越显著. 这种调整的作用效果不是一直有效的, 因为随着
将如图 4 所示变小因而低分 p 之间的差异也将缩小. 此外, 当 λ 提高到一定程度后, 高分区 p 将足以区分彼此, 再
继续增加 λ 值类边界也不会变化因而不会再影响检测结果.

2.3 漂移自适应
当发生突发事件或公众舆论开始改变时, 顺序到达的文本情感可能会显著波动, 在这种情况下, 当前模型不再
适合新的数据. 因此, 当漂移累积达到一定水平时, 应该对模型进行重新训练. 本文的漂移自适应策略基于“通知”
方法, 即当满足条件时激活触发器, 模型开始更新. 新模型采用基于 SPC [43] 的漂移检测方法, 漂移自适应采用一种
基于比较窗口 (CTW) 的记忆策略, 该策略决定哪些数据可以处理, 哪些数据可以放弃.
k
漂移自适应策略设置一个 n 大小的滑动窗口 W k , 用于保存历史信息, 其下标 表示与最近一次漂移发生的时