Page 67 - 《软件学报》2024年第6期

高猛 等: 位宽感知的寄存器绑定算法 2643

参数在 MiBench 测试集中进行测试, 实验结果表明, 单次连续多种着色达到 CMC 理论最优解的样例占比始终大
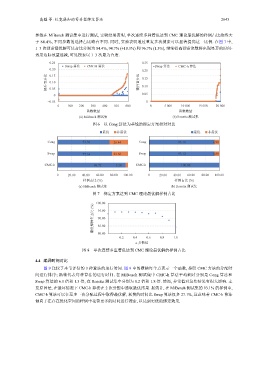
于 84.4%, 不同参数的选择占比略有不同. 同时, 实验表明通过重复多次搜索可以显著提高这一比例. 在图 7 中,
1–3 次搜索最优解可达占比分别为 84.4%, 94.7% (+10.3%) 和 96.7% (1.3%), 继续提高搜索次数将出现显著的时间-
效果边际效益递减, 可见搜索以 1–3 次最为合适.

0.25 0.25
Swap ෘم CMC-h ෘم Swap 算法 CMC-h ෘم
0.20 0.20
0.15
提升百分比 0.10 提升百分比 0.15
0.10
0.05
0 0.05
−0.05 0
0 100 200 300 400 500 600 0 5 000 10 000 15 000 20 000
函数数量 函数数量
图 8 单次连续多重着色达到
(a) MiBench 测试集 (b) Rosetta 测试集
图 6 以 Cong 算法为基线的绑定方案相对对比

最优 非最优 最优 非最优

Cong 73.56 26.44 Cong 93.10 6.90

Swap 77.34 22.66 Swap 93.12 6.88

CMC-h 96.72 3.28 CMC-h 100.00

0 20.00 40.00 60.00 80.00 100.00 0 20.00 40.00 60.00 80.00 100.00
样例占比 (%) 样例占比 (%)
(a) MiBench 测试集 (b) Rosetta 测试集
图 7 绑定方案达到 CMC 理论最优解样例占比

100.00
最优解样例占比 (%) 90.00
95.00

85.00
80.00
0.2 0.4 0.6 0.8 1.0
α ҕඔᆴ
CMC 理论最优解的样例占比

4.4 编译时间对比
图 9 比较了本节评估的 3 种算法的运行时间. 图 9 中的横轴每个点表示一个函数, 按照 CMC 方法的分配时
间进行排序; 纵轴代表每种算法的运行时间. 在 MiBench 测试集中 CMC-h 算法平均耗时分别是 Cong 算法和
Swap 算法的 6.1 倍和 1.5 倍, 在 Rosetta 测试集中分别为 8.2 倍和 1.8 倍. 然而, 异常值对这些结果有很大影响. 主
要原因是, 在最坏情况下 CMC-h 算法在 2 次分配中选取最优结果. 据统计, 在 MiBench 测试集的 93.1% 的样例中,
CMC-h 算法可以在至多一次分配过程中取得最优解, 耗费的时间比 Swap 算法仅多 27.1%, 这意味着 CMC-h 算法
倾向于在存在优化空间的样例中花费更多的时间进行搜索, 以达到更优的绑定效果.