Page 63 - 《软件学报》2024年第6期
P. 63
高猛 等: 位宽感知的寄存器绑定算法 2639
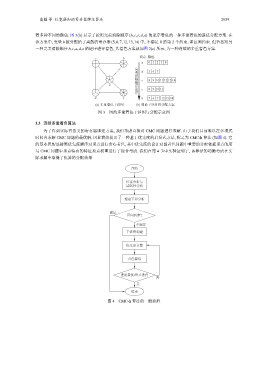
着多种不同的颜色. 图 3(b) 显示了按照完美消除顺序 {b,c,e,d,a} 的逆序着色的一种多重着色的最优分配方案. 在
该方案中, 变量 b 被分配给了离散的寄存器 {5,6,7,12,13,14} 中, 不满足 0 的第 2 个约束, 即区间约束. 但若按照另
一种完美消除顺序 b,c,a,d,e 的逆序进行着色, 其着色方案就如图 2(c) 所示, 为一种连续的多重着色方案.
c b 顶点 颜色
a 0 1 2 3 4
完美消除顺序逆序
d 5 6 7
e 8 9 10 11 12 13 14
a
c 8 9 10 11
d e b 5 6 7 12 13 14
(a) 多重着色干涉图 (b) 理论下界对应分配方案
图 3 图的多重着色干涉图与分配示意图
着色算法
3.3 连续多重着色算法
为了得到实际有意义的寄存器绑定方案, 我们考虑直接对 CMC 问题进行求解. 由于我们目前难以在多项式
时间内求解 CMC 问题的最优解, 因此我们提出了一种基于优先度的启发式方法, 称之为 CMC-h 算法 (如图 4). 它
的基本思想是按照优先度顺序对顶点进行贪心着色, 其中优先度的设计对图着色问题中重要的分配依据顶点的度
与 CMC 问题中顶点特有的特征顶点权重进行了综合考虑. 我们在第 4 节中实验证明了, 该算法的均衡考虑在实
际求解中取得了优异的分配效果.
开始
位宽分析与
活跃性分析
理论下界分析
满足
区间约束?
不满足
干涉图构建
优先度计算
理论最优/终止条件
否
是
结束
图 4 CMC-h 算法的一般流程