Page 301 - 《软件学报》2024年第4期

孙家泽 等: 基于可攻击空间假设的陷阱式集成对抗防御网络 1879

系, 促使对抗扰动指向陷阱类别标记的靶标可攻击空间, 从而进一步提升了 Trap-Net 的对抗防御效力. (3) 陷阱式
诱导因子应在不影响目标分类精度的基础上选取最大值.

Clean FGSM-before detecting PGD-after detecting Clean FGSM-before detecting PGD-after detecting
PGD-before detecting FGSM-after detecting PGD-before detecting FGSM-after detecting
100 100
80 80
Accuracy (%) 60 Accuracy (%) 60

40
40
20 20
0 0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Label smoothing factor Label smoothing factor
(a) 无目标攻击 (b) 有目标攻击
图 9 陷阱式诱导因子大小对防御效力影响

● RQ5: Trap-Net 相较于其他类似的对抗防御方法的防御效力如何?
为了进一步证明 Trap-Net 的对抗防御效力, 我们在相同的对抗攻击场景下, 对 Trap-Net 与核密度和贝叶斯不
确定性估计法, 特征压缩对抗防御方法和频谱对抗防御方法进行防御效力的对比. 在与核密度和贝叶斯不确定性
估计法的对比实验中, 我们以 Feinman 等人 [26] 的实验方式进行对抗样本和干净样本的探测比对. 将生成的对抗样
本和干净样本各自标记为独立的一类, 使用两种方法对其进行对抗样本的探测实验. 同时根据原实验评价标准, 使
用 AUC 值对模型的性能进行评估. 在与特征压缩的对比实验中, 我们以 7% 的误诊率计算阈值, 并使用 FGSM,
PGD 和 C&W 在不同扰动大小及有目标和无目标攻击场景下进行对抗防御方法的防御效力评估. 在与频谱对抗防
御方法的对比实验中, 我们使用 VGG16 网络模型, 以 CIFAR-10 为目标主体, CIFAR-100 为陷阱数据构建 Trap-Net.
将其与频谱对抗防御方法中所提出的高量傅里叶频谱防御方法 (MFS) 和阶段性傅里叶频谱防御方法 (PFS) 在不
同扰动大小的 FGSM, BIM, PGD 和 DeepFool 对抗攻击方法下进行模型对抗防御效力的评估.
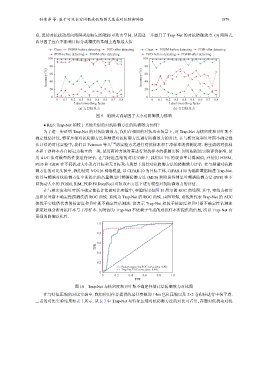
在与核密度和贝叶斯不确定性估计法的对比实验中, 实验结果如图 10 所示的 ROC 曲线图. 其中, 实线为核密
度和贝叶斯不确定性探测法的 ROC 曲线. 点线为 Trap-Net 的 ROC 曲线. 由图可知, 点线所代表 Trap-Net 的 AUC
值优于实线所代表的核密度和贝叶斯不确定性估测法. 这表示 Trap-Net 相较于核密度和贝叶斯不确定性估测法
能更好地分辨对抗样本与干净样本. 同时因为 Trap-Net 不依赖于生成的对抗样本所提供的信息, 所以 Trap-Net 有
更强的防御泛化性.

1.0
0.8

0.6
TPR
0.4
0.2
Feature squeezing ROC curve (area=0.87)
Trap-Net ROC curve (area=0.94)
0
0 0.2 0.4 0.6 0.8 1.0
FPR
图 10 Trap-Net 与核密度和贝叶斯不确定性估计法防御效力对比图

在与特征压缩的对比实验中, 我们使用作者提供的最佳参数即 1-bit 色位压缩以及 2×2 卷积核进行中值平滑.
二者的对比实验结果如表 7 所示. 从表 7 中 Trap-Net 与特征压缩对抗防御方法的对比可看出, 在面对低扰动对抗