Page 146 - 《软件学报》2021年第10期

3118 Journal of Software 软件学报 Vol.32, No.10, October 2021

[0.1,0.2])的效果都是可接受的.
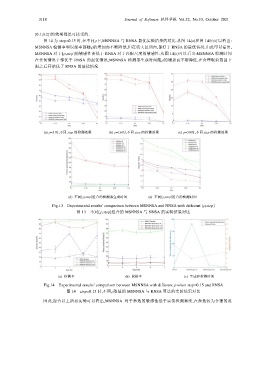
图 14 为 step=0.15 时,在不同下,MSNNSA 与 RNSA 最优实验结果的对比.从图 14(a)和图 14(b)可以看出:
MSNNSA 检测率和误报率都随的增加而不断降低,但在较大区间内,都好于 RNSA 的最优情况.由此可以看出,
MSNNSA 对于[,step]的敏感性要低于 RNSA 对于匹配尺度的敏感性.从图 14(c)可以看出:MSNNSA 检测时间
在任何情况下都优于 RNSA 的最优情况;MSNNSA 检测器生成时间随的增加而不断降低,在合理取值范围下
限之后开始优于 RNSA 的最优情况.

(a) =5 时,不同 step 的检测效果 (b) =16 时,不同 step 的检测效果 (c) =30 时,不同 step 的检测效果

(d) 不同[,step]组合的检测器生成时间 (e) 不同[,step]组合的检测时间
Fig.13 Experimental results’ comparison between MSNNSA and NNSA with different [,step]
图 13 不同[,step]组合的 MSNNSA 与 NNSA 的实验结果对比

(a) 检测率 (b) 误报率 (c) 生成和检测时间
Fig.14 Experimental results’ comparison between MSNNSA with different  when step=0.15 and RNSA
图 14 step=0.15 时,不同取值的 MSNNSA 与 RNSA 算法的实验结果对比

因此,综合以上所有实验可以看出,MSNNSA 对于参数的敏感性低于实值检测算法,在参数较为合理的范