Page 330 - 《软件学报》2021年第9期

2954 Journal of Software 软件学报 Vol.32, No.9, September 2021

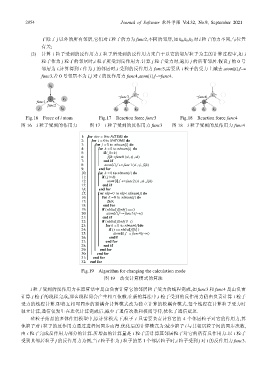
子除了 j 以外的所有邻居,它们对 i 粒子的力为 func2,不同的邻居,如 k 0 ,k 1 ,k 2 对 i 粒子的力不同,与位置
有关;
(2) 计算 i 粒子受到的反作用力.i 粒子所受到的反作用力来自于以它的邻居粒子为主的计算过程中,如 i
粒子作为 j 粒子的邻居时,i 粒子所受到反作用力.计算 j 粒子受力时,遍历 j 的所有邻居.假设 j 的 0 号
邻居为 i,计算得到 i 作为 j 的邻居时,i 受到的反作用力 func3,需要从 i 粒子的受力上减去.atom[i].f−=
func3.若 0 号邻居不为 i,j 对 i 的反作用力 func4,atom[i].f−=func4.

k 2
i i
i k 1 -func3 -func4
func1 j j
func2
j k 0
k 0 k 1 k 2 k 0 k 1 k 2
Fig.16 Force of i atom Fig.17 Reaction force func3 Fig.18 Reaction force func4
图 16 i 粒子受到的作用力 图 17 i 粒子受到的反作用力 func3 图 18 i 粒子受到的反作用力 func4

1: for iter = 0 to NITERS do
2: for i = 0 to NATOMS do
3: for j = 0 to nbnum[i] do
4: for k = 0 to nbnum[i] do
5: if ( j != k)
6: fijk = func0(si , sj , sk)
7: end if
8: atom[i].f += func1(si , sj , fijk)
9: end for
10: for k = 0 to nbnum[i] do
11: if ( j != k)
12: atom[i].f += func2(si , sk , fijk)
13: end if
14: end for
15: for nbj =0 to nbj< nbnum[j] do
16: for k = 0 to nbnum[j] do
17: Zk0;
18: end for
19: if (nblist[j][nbj] == i)
20: atom[i].f -= func3(j→i)
21: end if
22: if nblist[j][nbj] != i)
(
23: for k = 0 to nbnum[j] do
24: if (i == nblist[j][k] )
25: atom[i].f -= func4(j→i)
26: endif
27: end for
28: end if
29: end for
30: end for
31: end for
32: end for
Fig.19 Algorithm for changing the calculation mode
图 19 改变计算模式的算法

i 粒子受到的反作用力在原算法中是由负责计算它的邻居粒子受力的线程完成,如 func3 和 func4 是由负责
计算 j 粒子的线程完成,那么线程间会产生相互依赖.在新的算法中,i 粒子受到的反作用力仍由负责计算 i 粒子
受力的线程计算.即将互相写同步的紧耦合计算模式改为独立计算的松耦合模式.每个线程在计算粒子受力时
独立计算,通信仅发生在迭代计算完成后,减少了通信次数和核间等待,优化了通信延迟.
硅粒子结晶的多体作用模型中,原计算模式下,粒子 i 只需要负责计算它的 4 个邻居粒子对它的作用力,其
他粒子对 i 粒子的反作用力通过进程间同步而得.优化后的计算模式为:减少粒子 i 与其邻居粒子间的同步次数,
由 i 粒子完成反作用力部分的计算.所增加的计算量是 i 粒子需计算其邻居粒子对它的所有反作用力.以 i 粒子
受到其邻居粒子 j 的反作用力为例,当 i 粒子作为 j 粒子的第 1 个邻居粒子时,i 粒子受到 j 对 i 的反作用力 func3.