Page 247 - 《软件学报》2020年第11期

3562 Journal of Software 软件学报 Vol.31, No.11, November 2020

平均二跳共同邻居数目

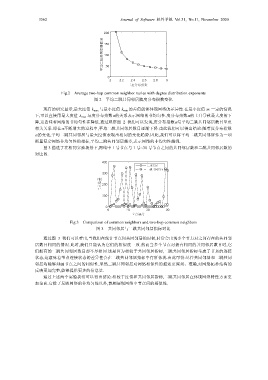
Fig.2 Average two-hop common neighbor varies with degree distribution exponents
图 2 平均二跳共同邻居随度分布指数变化

现有的研究显示,最大度值 k max 与最小度值 k min 的差值能够体现网络的差异性.在最小度值 m 一定的情况
下,可以直接用最大度值 k max 与度分布指数α的关系表示网络的非均匀性.度分布指数α的上升导致最大度的下
降,这意味着网络的非均匀性在降低.通过观察图 2 我们可以发现,度分布指数α与平均二跳共同邻居数目呈负
相关关系.即在α不断增大的过程中,平均二跳共同邻居数目逐渐下降.由此我们可以得出结论:随着度分布指数
α的变化,平均二跳共同邻居与最大度值表现出相同的变化趋势.因此,我们可以将平均二跳共同邻居作为一项
衡量复杂网络非均匀性的指标,平均二跳共同邻居越多,表示网络的非均匀性越强.
图 3 描述了在相同实验场景下,网络中 1 号节点与 1 号~30 号节点之间的共同邻居数和二跳共同邻居数的
对比图.

Fig.3 Comparison of common neighbors and two-hop common neighbors
图 3 共同邻居与二跳共同邻居指标对比
通过图 3 我们可以看出,当我们在统计节点间共同邻居的时候,时常会出现多个节点对之间存在的共同邻
居数目相同的情况.此时,我们只能认为它们的相似度一致.然而当多个节点对拥有相同的共同邻居数目时,它
们拥有的二跳共同邻居数目却不尽相同.这是因为相较于共同邻居指标,二跳共同邻居指标考虑了节点的连接
状态,这意味着节点连接状态的差异性会在二跳共同邻居指标中有所体现.由此可得:尽管共同邻居和二跳共同
邻居均能够刻画节点之间的相似性,显然二跳共同邻居对网络相似性的描述更深刻、准确,对网络拓扑结构的
反映更加完整,能够提供更多的信息量.
通过上述两个实验我们可以得出结论:相较于度值和共同邻居指标,二跳共同邻居在体现网络特性方面更
加全面.它除了反映网络的非均匀性以外,兼顾展现网络中节点间的相似性.