Page 240 - 《软件学报》2020年第11期

尹子都 等:基于采样的在线大图数据收集和更新 3555

0.6 的效果最好.总体上,β为 0.2 时效果最好,对应曲线与坐标轴之间所构成区域的面积最大.由此可知,对于不同
的数据集,应选取合适的α和β.
4.3 效率测试
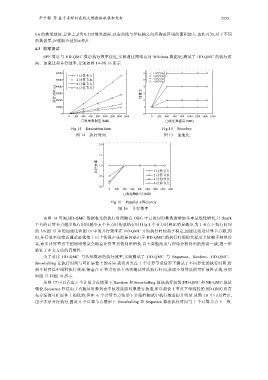
EPP 算法与 HD-QMC 算法执行效率接近,实验通过网络访问 Wikidata 数据集,测试了 HD-QMC 的执行时
间、加速比和并行效率,分别如图 14~图 16 所示.

60000 6 1 计算节点
1 计算节点 2 计算节点
50000 2 计算节点 5 4 计算节点
6 计算节点
4 计算节点 4
40000
执行时间 (s) 30000 加速比 3 2
6 计算节点
20000
10000 1
0 0
0 200 400 600 800 1000 1200 1400 1600 0 200 400 600 800 1000 1200 1400 1600
已收集数据量 (MB) 已收集数据量 (MB)
Fig.14 Execution time Fig.15 Speedup
图 14 执行时间 图 15 加速比

2.0
1.5
并行效率 1.0 1 计算节点

0.5 2 计算节点
4 计算节点
6 计算节点
0.0
0 200 400 600 800 1000 1200 1400 1600
已收集数据量 (MB)
Fig.16 Parallel efficiency
图 16 并行效率

由图 14 可知,HD-QMC 数据收集的执行时间随着 OBG 中已访问对象数的增加基本呈线性增长,且 Spark
平台的计算节点越多执行时间越少,6 个节点时的总执行时间与 1 个节点时相比明显减少,为 1 节点下执行时间
的 1/6.图 15 中的加速比和图 16 中的并行效率在 HD-QMC 开始执行时便趋于稳定,加速比接近计算节点数,同
时,并行效率也接近理论最优值 1.以上情况产生的原因是由于 HD-QMC 的执行时间很大程度上依赖于网络带
宽,而多计算节点下的网络带宽会随着计算节点数同步增长.以上实验结果与理论分析得出的结论一致,进一步
验证了本文方法的高效性.
为了对比 HD-QMC 与传统算法的执行效率,实验测试了 HD-QMC 与 Sequence、Random、HD-QMC、
Snowballing 在执行时间与可扩展性上的差异.我们首先在 1 个计算节点情形下测试了不同算法的执行时间,得
到不同算法单线程执行效率.接着在 6 节点情形下再次测试算法执行时间,获取不同算法的可扩展性表现,分别
如图 17 和图 18 所示.
从图 17 可以看出,1 个计算节点情形下,Random 和 Snowballing 算法执行较慢,HD-QMC 和 BB-QMC 算法
稍快,Sequence 算法由于直接从对象列表中依次选取对象进行获取,所以最快.1 节点下单线程的 HD-QMC 没有
充分发挥可扩展性上的优势,但在 6 个计算节点情形下多线程测试中执行效率提升明显.从图 18 中可以看出,
由于无法并行执行,因此 6 个计算节点情形下 Snowballing 和 Sequence 算法执行时间与 1 个计算节点下一致.