Page 115 - 《摩擦学学报》2021年第5期

704 摩 擦 学 学 报 第 41 卷

80
(a) (b)
5 Conical probe
70
Spherical probe
60
4 50
Friction/nN 3 2 F adh /nN 40 Conical probe
Spherical probe
30
20
1
10
0 0
0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2
Thickness/nm Thickness/nm

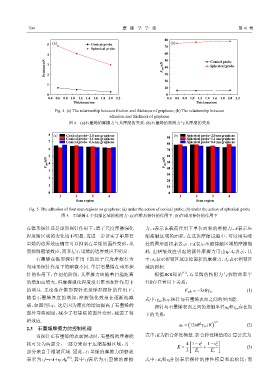
Fig. 4 (a) The relationship between friction and thickness of graphene; (b) The relationship between
adhesion and thickness of graphene
图 4 (a)石墨烯的摩擦力与其厚度的关系；(b)石墨烯的粘附力与其厚度的关系

8 (a) Conical probe−2.0 nm graphene (b) Spherical probe−2.0 nm graphene
Conical probe−1.1 nm graphene 90 Spherical probe−1.1 nm graphene
7 Conical probe−0.6 nm graphene Spherical probe−0.6 nm graphene
80
6 70
5 60
F adh /nN 4 F adh /nN 50

3 40
30
2
20
1
10
0 0
1 2 3 4 1 2 3 4
Scan region Scan region

Fig. 5 The adhesion of four scan regions on graphene: (a) under the action of conical probe; (b) under the action of spherical probe
图 5 石墨烯 4 个扫描区域的粘附力: (a)在锥形探针的作用下; (b)在球形探针的作用下

在锥形探针还是球形探针作用下，原子尺度摩擦强化 力，τ表示在载荷作用下单位面积的摩擦力，A表示压
程度随区域的变化均不明显. 这进一步证实了单层石 缩接触区域的面积，在这次摩擦试验中，可以用尖峰
墨烯的边界效应确实可以抑制石墨烯的面外变形，从 处的圆形面积来表示. τ·A表示压缩接触区域的摩擦能
而抑制褶皱效应，而多层石墨烯的边界效应不明显. 耗. 由褶皱效应引起的额外摩擦力可由τ ·A 表示，其
P
P
石墨烯在锥形探针作用下的原子尺度摩擦行为 中：τ 表示褶皱区域单位面积的摩擦力，A 表示褶皱区
P P
与球形探针作用下的略微不同. 单层石墨烯在球形探 域的面积.
针的作用下，在初始阶段，其摩擦力也随着扫描距离 根据JKR理论 ，石墨烯的粘附力与探针曲率半
[31]
的增加而增大，但摩擦强化程度没有锥形探针作用下 径R存在着以下关系：
的明显. 无论是在锥形探针还是球形探针的作用下， F adh = −3πRγ sv (1)
随着石墨烯厚度的增加，摩擦强化效果在逐渐地减
式中：γ 表示探针与石墨烯表面之间的界面能.
sv
弱，如图7所示. 这是因为厚度的增加提高了石墨烯的 探针与石墨烯表面之间的接触半径a 和γ 存在如
0
sv
面外弯曲刚度，减少了石墨烯的面外变形，减弱了皱 下的关系：
褶效应. ( ) 1/3
2
a 0 = 12πR γ sv /K (2)
2.3 石墨烯摩擦力的控制机理
当探针在石墨烯的表面滑动时，石墨烯的摩擦能 式中：K为折合弹性模量. 折合弹性模量的计算公式为
[
耗可分为两部分，一部分来自于压缩接触区域，另一 4 1−v 2 t 1−v 2 s ]
K = + (3)
部分来自于褶皱区域. 因此，石墨烯的摩擦力能够被 3 E t E s
表示为：f=τ·A+τ ·A P [30] , 其中：f表示为石墨烯的摩擦 式中：E 和ν 分别表示探针的弹性模量和泊松比；而
P
t
t