Page 7 - 《摩擦学学报》2021年第1期

4 摩 擦 学 学 报 第 41 卷

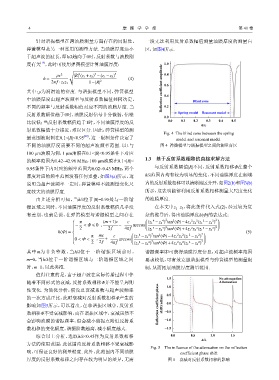
针对谐振模型在薄油膜测量方面存在的局限性， 一段无法利用反射系数幅值测量油膜厚度的测量盲
弹簧模型是另一种常用的测量方法. 当油膜厚度远小 区，如图4所示.
于超声波的波长，即h/λ趋向于0时，反射系数与油膜刚

[19]
度有关 ，此时可使用弹簧模型计算油膜厚度： 1.0
√
2
2
ρc 2 |R| (z 1 +z 3 ) −(z 1 −z 3 ) 2 0.8
h = (4)
2πf ·z 1 z 3 1−|R| 2 0.6
其中：ρ为润滑油的密度. 与谐振模型不同，弹簧模型 Reflection coefficient amplitude
中油膜厚度由超声波频率与反射系数幅值共同决定， 0.4 Blind zone
不同的频率与反射系数幅值对应不同的油膜厚度. 当 0.2
反射系数幅值趋于0时，油膜反射信号十分微弱，信噪 Spring model Resonant model
0.0
比较低；当反射系数幅值趋于1时，不同油膜厚度的反 0.0 0.1 0.2 0.3 0.4 0.5
h/λ
射系数幅值十分接近，难以区分. 因此，弹簧模型的测
Fig. 4 The blind zone between the spring
[20]
量范围被限制在0.1<|R|<0.95 ，这一限制条件决定了 model and resonant model
不同的油膜厚度需要不同的超声波频率范围. 以1与 图 4 弹簧模型与谐振模型之间的测量盲区
100 μm油膜为例，1 μm油膜在0.1<|R|<0.95条件下对应
1.3 基于反射系数相移的直接求解方法
的频率范围为1.42~42.96 MHz，100 μm油膜在0.1<|R|<
0.95条件下内对应的频率范围为0.02~0.43 MHz，两个 与反射系数幅值|R|不同，反射系数相移Φ在整个
厚度对应的频率范围没有任何重叠，如图3(a)所示，这 h/λ范围内均有较为明显的变化，不同油膜厚度在频域
说明当超声波频率一定时，弹簧模型不能测量变化尺 内的反射系数相移可以清晰地区分开，如图2(b)和图3(b)
度较大的油膜厚度. 所示，这表明能够利用反射系数相移测量大尺度变化
由上述分析可知，当h/λ位于|R|=0.95处与一阶谐 的油膜厚度.
振区域之间时，不同油膜厚度的反射系数幅值几乎没 在本文中z =z ，将此条件代入式(2)，经过较为复
3
1
有差别，也就是说，在弹簧模型与谐振模型之间存在 杂的推导后，得出油膜厚度h(Φ)的表达式：
  4 4 2 2 2 2 2 2 2 
 π (m+1)c c  (z 1 −z 2 ) tan (Φ)−4z 1 z 2 (z 1 −z 2 ) 
  

− < Φ ⩽ 0 , − arccos   
  4 2 2 2 
 2 2 f 4πf 4 2 2 2 2
 (z 1 −z 2 ) tan (Φ)+4z 1 z 2 (z 1 −z 2 )

(5)
h(Φ) =   
 4 4 2 2 2 2 2 2 2
 mc
 π c  (z 1 −z 2 ) tan (Φ)−4z 1 z 2 (z 1 −z 2 )  


0 < Φ < , + arccos   

  4 2 2 2 
2 2 f 4πf (z 1 −z 2 ) tan (Φ)+4z 1 z 2 (z 1 −z 2 )
2
2
2
2
4
其中m为非负整数，当h/λ位于一阶谐振区域前时， 谐振频率即可获得油膜厚度信息，对超声波频率范围
m=0，当h/λ位于一阶谐振区域与二阶谐振区域之间 要求较低，可有效克服谐振模型与弹簧模型的测量限
时，m=1，以此类推. 制，从而拓展油膜厚度测量范围.
值得注意的是，由于超声波在实际传播过程中伴
1.5 No attenuation
随着不同形式的衰减，反射系数相移Φ并不能呈周期 Attenuation
性变化. 为简化分析，假设总衰减系数与超声波频率 1.0
的一次方成正比，此时衰减对反射系数相移Φ产生的 0.5
影响如图5所示，可以看出，在非谐振区域中，反射系 Reflection coefficient phase shift/radians 0.0
数相移Φ不受衰减影响，而在谐振区域中，衰减虽然不 −0.5
会影响油膜的谐振频率，但会减小谐振点附近反射系 −1.0
数相移的变化幅度，谐振阶数越高，减小幅度越大. −1.5
综合以上分析，选取h/λ<0.45作为反射系数相移 0.0 0.5 1.0 1.5
h/λ
方法的使用范围，此范围内反射系数相移不受衰减影
Fig. 5 The influence of the attenuation on the reflection
响，可保证良好的测量精度. 此外，此范围内不同油膜 coefficient phase shift
厚度的反射系数相移之间存在较为明显的差异，无需 图 5 衰减对反射系数相移的影响