Page 79 - 《高原气象》2025年第3期

3 期 李 健等：基于CMA-GD模式的2 m气温逐小时预报误差订正方法分析 637

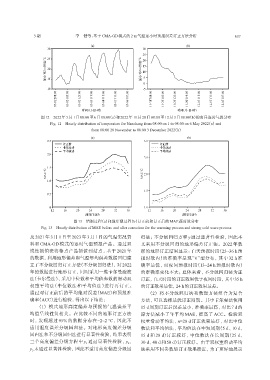
图12 2022年5月1日08:00至6日08:00（a）和2022年11月28日08:00至12月3日08:00（b）的南昌逐时气温分布
Fig. 12 Hourly distribution of temperature for Nanchang from 08:00 on 1 to 08:00 on 6 May 2022（a） and
from 08:00 28 November to 08:00 3 December 2022（b）

图13 增温过程（a）和强寒潮过程（b）订正前和订正后的MAE逐时效分布
Fig. 13 Hourly distribution of MAE before and after correction for the warming process and strong cold wave process
及 2021 年 3 月 1 日至 2023 年 3 月 1 日的气温实况资 归法； 不分级回归方程 y 通过显著性检验， 因此本
料和 CMA-GD 模式的逐时气温预报产品。通过双 文采用不分级回归的地形偏差订正法。2022 年数
线性插值法将格点产品插值到站点， 基于 2021 年 据的地形订正结果显示： 白天预报时段（25~36 h 预
的数据， 利用地形偏差和气温年均误差数据回归建 报时效内）的准确率呈现“V”型分布， 其中 32 h 准
立了不分级回归订正方法（不分级回归法）， 对 2022 确率最低， 而夜间预报时段（13~24 h 预报时效内）
年的数据进行地形订正， 同时采用一维卡尔曼滤波 的准确率变化不大； 总体来看， 不分级回归法为正
法（卡尔曼法）、 采用中位数和平均值参数的滑动双 订正， 白天时段的订正效果优于夜间时段， 其中35 h
权重平均法（中位数法和平均值法）进行再订正。 的订正效果最佳， 24 h的订正效果最差。
通过对订正前后的平均绝对误差（MAE）和预报准 （2） 将不分级回归法和数理方法组合为复合
确率（ACC）进行检验， 得出以下结论： 方法， 可以选择最优订正周期。其中卡尔曼法使用
（1） 模式地形高度偏差与预报的气温误差平 15 d周期订正后误差最小， 准确率最高， 对比 7 d的
均值呈线性负相关。在比较不同的地形订正方法 原方法减小了年平均 MAE， 提高了 ACC。检验双
时， 发现超过 95% 的数据分布在-2~2 ℃， 因此不 权重滑动平均法， n=20 d 订正效果最好， 对比中位
适用温度误差分级回归法。对地形高度偏差分级 数法和平均值法， 平均值法在中短周期（5 d、 10 d、
回归法和不分级回归法进行显著性检验， 结果表明 15 d 和 20 d）订正较好， 中位数法在长周期（25 d、
三个高度偏差分级方程中 y 1 通过显著性检验， y 2 、 30 d、 40 d和 50 d）订正较好。由于双权重滑动平均
y 3 未通过显著性检验， 因此不适用高度偏差分级回 法采用不同参数后订正效果接近， 为了更好地展示