Page 18 - 《爆炸与冲击》2026年第01期

第 46 卷 李 尧，等： 结构体高速倾斜入水的尾拍载荷及姿态稳定性 第 1 期

1.3 数值方法验证
开展入水结构体高速入水计算前首先进行数值模型验证，参照 Chen 等 [14] 开展的高速入水姿态稳定
性实验，将空泡形态及入水深度作为验证参数。将方形计算域划分为空气域和水域，计算域的边界条件
主要包括速度入口、压力出口、对称边界。这里采用三套网格（分别为粗网格、中等网格和细网格）对计
算流体域进行划分，粗网格、中等网格和细网格分别指采用 0.2、0.125 和 0.06 倍的入水结构体直径作为
入水结构体头部、尾部及附件表面网格的最小尺寸。为了保证模型的准确性，对自由表面、入水结构体
垂直入水经过的区域附近进行了网格加密。利用粗网格、中等网格和细网格对计算域划分后的网格总
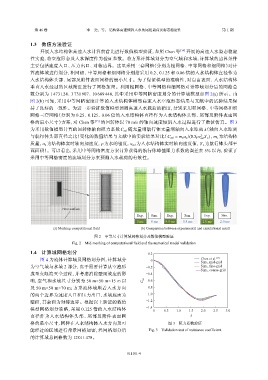
数分别为 1 473 124、3 731 907、10 689 440，其中采用中等网格密度划分的计算域模型如图 2(a) 所示。由
图 2(b) 可知，采用中等网格密度计算的入水结构体模型高速入水空泡形态结果与文献中的试验结果保
持了良好的一致性。为进一步验证数值模型预测高速入水载荷的精度，分别采用粗网格、中等网格和细
网格三套网格（分别为 0.25、0.125、0.06 倍的入水结构体直径作为入水结构体头部、尾部及附件表面网
格的最小尺寸）方案，对 Chen 等 [23] 的回转体以 70 m/s 的轴向速度倾斜入水过程进行了数值仿真。图 3
λ （轴向入水距离
为采用数值模型计算的回转体轴向阻力系数 C axl 随无量纲航行体无量纲轴向入水距离
C axl = m c a x /(0.5ρv S c ) m c 为结构体
2
axl
与航行体头部直径之比）变化的数值结果与文献中的实验结果对比（ ，
S c 为航行体头部平
质量， a x 为结构体实时轴向加速度， ρ 为水的密度， v axl 为入水结构体实时轴向速度值，
面面积）。可以看出，采用中等网格密度方案计算获得的航行体峰值阻力系数的误差在 5% 以内，验证了
采用中等网格密度的流域划分方案预测入水载荷的有效性。

Free surface
Exp. Sim. Exp. Sim. Exp. Sim.
0 ms 0 ms 0.8 ms 0.8 ms 2.0 ms 2.0 ms
(a) Meshing computational field (b) Comparison between experimental and simulational result

图 2 中等尺寸计算域网格划分及数值模型验证
Fig. 2 Mid-meshing of computational field and the numerical model validation

1.4 计算域网格划分 0.2
图 4 为流体计算域及网格划分图，计算域分 0 Chen et al. [23]
Sim., mid-grid
为空气域与水域 2 部分，由于需要计算从空泡形 −0.2 Sim., fine-grid
Sim., coarse-grid
成至夹断溃灭全过程，并考虑消除壁面效应的影 −0.4
响，空气和水域尺寸分别为 50 m×50 m×15 m 以 C axl −0.6
及 50 m×50 m×70 m；方形流体域顺着入水方向 −0.8
的两个边界为速度入口和压力出口，水域底面为 −1.0
壁面，其余面为对称边界。根据以上验证的数值 −1.2
模型网格划分策略，采用 0.125 倍的入水结构体 −1.4 0 0.5 1.0 1.5 2.0 2.5 3.0
直径作为入水结构体头部、尾部及附件表面网 λ
格的最小尺寸，同样在入水结构体入水方向及可 图 3 阻力系数验证
能经过的区域进行背景网格加密，经网格划分后 Fig. 3 Validation test of resistance coefficient
的计算域总网格数为 12 011 478。

011101-4