Page 176 - 《爆炸与冲击》2026年第01期

第 46 卷 伍俊英，等： 金属桥箔电爆炸驱动飞片过程流场瞬态观测与数值模拟 第 1 期

»
( ) 2
Cu
−K + K 1 Cu +4K 1 Cu
1
Cu
α =
e
2
Å ã 3/2 Å Cu Cu ã
I − I 0
Cu
3/2
1
K 1 = T exp − (14)
2u Cu +
2πm e k B m Cu +
Cu
2
n u Cu 0 h m Cu 0 k B T
式中：K 为一级电离平衡常数。
1
计算中，将等离子体状态方程和热力学性质的表达式嵌入到计算程序中，从而模拟等离子体的膨胀
扩散过程。
2.2.3 飞片运动的描述
采用动网格模型描述流场驱动下飞片运动的计算过程中，在每一个时间步内，计算模型均会求解出
飞片附近区域流场的压力，计算出飞片受力边界处的推力，然后通过阻力系数得到飞片受到的阻力，进
而得到飞片受到的合力，从而计算出飞片的加速度。加速度与时间步长的乘积为飞片在一个时间步长
内的速度增量，前一个时间步计算得到的速度与该时间步内速度增量之和为飞片的最新速度，根据飞片
的速度、加速度以及时间步长可以计算得到飞片的最新位置。在获得飞片的最新位置后，计算模型按照
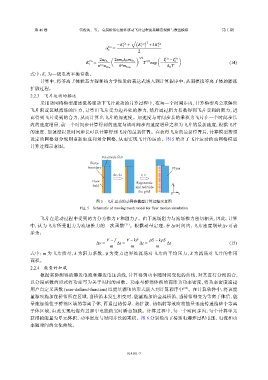
设定的网格划分规则重新生成和划分网格，从而实现飞片的运动。图 5 给出了飞片运动的动网格模型
计算过程示意图。

Polyimide film
Force
boundary Flyer
dv, dx v, x
Flow
Regenerate
field y
and redivide
the grid
O x
图 5 飞片运动的动网格模型计算过程示意图
Fig. 5 Schematic of moving mesh model for flyer motion simulation

f 。由于流场阻力与流场推力密切相关，因此，计算
飞片在运动过程中受到的力分为推力 F 和阻力
中，认为飞片所受阻力为流场推力的一次函数 [21] 。根据动量定理，在 ∆t 时间内，飞片速度增量 ∆v 可表
示为：
F − f F −kF pS −kpS
∆v = ∆t = ∆t = ∆t (15)
m m m
式中：m 为飞片质量，k 为阻力系数， p 为受力边界处流场对飞片的平均压力，S 为流场对飞片的作用
面积。
2.2.4 能量的加载
根据实验测得的爆发电流和爆发电压曲线，计算得到功率随时间变化的曲线，对其进行分段拟合，
以分段函数的形式将功率写为关于时间的函数。功率与桥箔体积的商即为功率密度，将功率密度通过
用户自定义函数 (user-defined-function) 以能量源项的形式嵌入到计算程序中 [22] 。在计算软件中，将该能
量源项施加在桥箔所在区域，当桥箔未发生相变时，能量施加给金属桥箔，当桥箔相变为等离子体后，能
量施加给位于桥箔区域的等离子体，再通过热传导、热扩散、热辐射等效应将能量迅速传递给整个等离
子体区域，由此实现电爆炸过程中电能的实时瞬态加载。计算过程中，每一个时间步内，每个计算单元
获得的能量为单元体积、功率密度与时间步长的乘积。图 6 分别给出了桥箔电爆炸过程电压、电流和功
率随时间的变化曲线。

014101-7