Page 86 - 《爆炸与冲击》2025年第6期
P. 86
第 45 卷 王 伟,等: 循环冲击作用下砂岩裂缝扩展及渗透率响应特征 第 6 期
0.10 Incident wave 150 σ In
Transmitted wave 100 σ Re
0.05 Reflected wave 50 σ Tr
σ In +σ Re
Signal voltage/V −0.05 0 Stress/MPa −50 0
−100
−0.10
−150
−0.15
−200
−0.20 −250
0 0.2 0.4 0.6 0.8 1.0 0 50 100 150 200 250 300
Time/ms Time/μs
图 5 SHPB 原始波形 图 6 应力平衡图
Fig. 5 SHPB original waveform Fig. 6 Stress balance diagram
试样在 9 次冲击过程中的动态应力-应变曲线见图 7。动态应力-应变曲线呈现明显的阶段性变化特
征,起初近似为直线(处于弹性变形阶段),之后曲线趋缓进入塑性变形阶段,接下来发生破坏进入峰后
卸载阶段,应变呈现逐渐减小的趋势,出现明显的“回弹”现象。但是,随着冲击次数的增加,动态应力-
应变曲线在弹性变形阶段之前出现压密阶段,表现为在应力随应变增加缓慢(冲击 3~7 次)或基本维持
不变(冲击 8~9 次)。这是因为原始试样较致密、无明显孔裂缝发育,近似于弹性体,受载未被压缩。在
冲击 3~7 次后,试样内产生少量冲击裂缝,动荷载加载后裂缝首先压缩闭合;在冲击 8~9 次后,试样内
部冲击裂缝大量发育,导致动荷载主要消耗于将压密裂缝,压密阶段最明显。
100
1st
80 Elastic stage 2nd
3rd
4th
60 5th
6th
Stress/MPa 40 7th
8th
9th
20
0
Compaction stage Elastic stage
−20
0 5 10 15 20 25 30 35 40
Strain/10 −3
图 7 砂岩试样应力-应变曲线
Fig. 7 Stress strain curves of samples
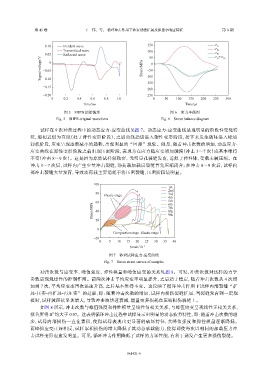
冲击次数与应变率、峰值强度、弹性模量和峰值应变的关系见图 8。可见,冲击次数对试样的力学
参数呈现规律性的控制作用。前两次冲击平均应变率明显提升,之后趋于稳定,随着冲击次数从 4 次增
加到 7 次,平均应变率再次迅速升高,之后基本维持不变。这反映了循环冲击作用下试样内部裂缝“扩
展-压实-再扩展-再压实”的过程,即:随着冲击次数的增加,试样内损伤裂缝扩展,当裂缝发育到一定规
模时,试样波阻抗显著增大,导致冲击波快速衰减,能量更多损耗在压缩损伤裂缝上。
如图 8 所示,冲击次数与峰值强度和弹性模量呈线性负相关关系,与峰值应变呈现线性正相关关系,
拟合所得 R 均大于 0.97。这表明循环冲击过程中试样显示出明显的动态疲劳特性,即:随着冲击次数的增
2
多,试样内部损伤一直在累积,使得试样表现出更显著的破坏特征,其峰值强度和弹性模量逐渐降低。
而峰值应变正好相反,试样累积损伤的增大降低了其动态承载能力,使得即使每次以相同的加载压力冲
击试样变形也愈发明显。可见,循环冲击作用降低了试样的力学性能,有利于诱发产生更多损伤裂缝。
061421-6