Page 20 - 《爆炸与冲击》2025年第6期

第 45 卷 马泗洲，等： 围压与爆破耦合作用下节理岩体裂纹的扩展行为与影响因素 第 6 期

3.4 动态应力强度因子 v y
通常情况下，不连续面尖端更容易出现应 θ=π
力集中，从而导致材料起裂扩展。采用动态应力 u Node
Tip
强度因子（dynamic stress intensity factor, DSIF）可 r
r i θ=−π
以解释节理岩体在围压与爆破耦合作用下的裂
θ
纹扩展机制。动态应力强度因子可以通过解析 x
法、实验法或数值法获得，本文通过有限元数值
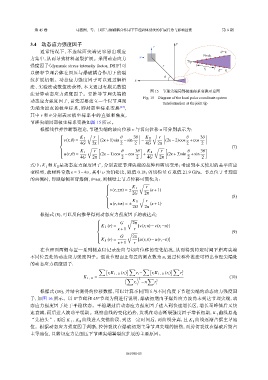
图 15 节理尖端局部极坐标系变换示意图
法计算动态应力强度因子。要推导节理尖端的
Fig. 15 Diagram of the local polar coordinate system
动态应力强度因子，首先需要建立一个以节理面
transformation at the joint tip
尖端为原点的极坐标系，即局部坐标系变换 [27] ，
其中 r 和 θ 分别表示极坐标系中的直径和角度，
节理尖端局部极坐标系变换如图 15 所示。
根据线性弹性断裂理论，节理尖端的法向位移 ν 与切向位移 u 可分别表示为：
 … ï ò … ï ò
K Ⅰ r θ 3θ K Ⅱ r θ 3θ

v(r,θ) = (2κ +1)sin −sin − (2κ −2)cos +cos

 4G 2π 2 2 4G 2π 2 2
(7)
… ï ò … ï ò
 r θ 3θ r θ 3θ
 K Ⅰ K Ⅱ
u(r,θ) = (2κ −1)cos −cos + (2κ +3)sin +sin

4G 2π 2 2 4G 2π 2 2
式中：K 和 Ⅰ K 是动态应力强度因子，分别表征节理尖端的拉伸和剪切变形；考虑到本文使用的是平面应
Ⅱ
κ = 3−4υ ，其中 υ 为泊松比，取值 0.18；剪切模量 取值 21.9 GPa。节点位于节理面
变模型，故材料常数 G
的两侧时，即迎爆侧和背爆侧，θ=±π，则侧壁上节点位移可简化为：

…
K Ⅰ r

v(r,±π) = ± (κ +1)

2G 2π

(8)
…
 r
 K Ⅱ

u(r,±π) = ± (κ +1)
2G 2π
根据式 (8)，可以反向推导得到动态应力强度因子的表达式：

…
G 2π

 K Ⅰ (r) = [v(r,π)−v(r,−π)]

κ +1 r

(9)
…

 G 2π

 K Ⅱ (r) = [u(r,π)−u(r,−π)]
κ +1 r
在节理面两侧布置一系列测点以记录法向与切向位移的变化情况，从而得到特定时间下距离尖端
不同位置处的动态应力强度因子。假设节理面上布置的测点数为 n，通过位移外推法可得出节理尖端处
的动态应力强度因子：
] ∑ ] ∑
∑ [ ∑ [
r i K Ⅰ,Ⅱ (r i ) r i − r i K Ⅰ,Ⅱ (r i ) r 2 i
K Ⅰ,Ⅱ = (10)
Ä∑ ä 2 ∑
−n r 2
r i
i
根据式 (10)，并结合测得的位移数据，可以计算不同围压与不同角度下节理尖端的动态应力强度因
子，如图 16 所示。以 0°节理和 45°节理为例进行说明，爆破初期由于爆炸应力波尚未到达节理尖端，动
态应力强度因子处于平稳状态。平稳期过后动态应力强度因子进入到快速增长区，增长至峰值后又快
速衰减，而后进入波动平缓期。观察曲线的变化趋势，发现在动态断裂强度因子增长初期，K 曲线总是
Ⅰ
“先抬头”，而后 K 、K 曲线进入交错阶段，到达一定时间后，两曲线分离，且 K 曲线逐渐占据主导地
Ⅰ
Ⅱ
Ⅱ
位。根据动态应力强度因子判断，拉伸裂纹在爆破初期主导节理尖端的损伤，而剪切裂纹在爆破后期占
主导地位，且剪切应力是围压下节理尖端翼裂纹扩展的主要原因。

061001-15