Page 15 - 《爆炸与冲击》2025年第5期

第 45 卷 王 帅，等： 锯齿外形对弹体带攻角侵彻横向过载的影响 第 5 期

上锯齿面横向接触力先迅速减小再缓慢增大，最大值出现在最接近弹头的锯齿，其峰值为 50.1 kN；下锯
齿面的横向接触力持续减小，且由最接近弹头的 2 个锯齿承受，其峰值仅分别为 7.8、6.7 kN，明显小于上
锯齿面的峰值最大值，如图 13（c）所示。由于不同 V 形环槽锯齿的接触力也主要由上锯齿面承受，因而
从弹尖至弹尾，锯齿弹上下锯齿面横向力合力的分布也与上锯齿面分布相似，如图 13（d）所示。

2.4 接触力矩及弹道偏转机制
锯齿弹相比于光滑弹的另一个显著运动特征在于锯齿弹具有更大的偏转角，为此，进一步分析两种
弹体与靶体接触过程中所产生的接触力矩的差异，进而揭示锯齿弹的弹道偏转机制。
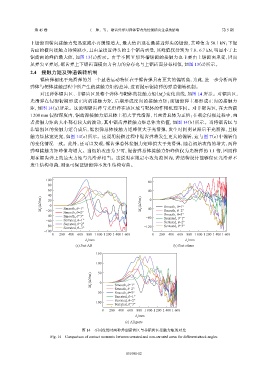
对比弹体锯齿区、非锯齿区及整个弹体与靶体的接触力矩（M ）变化曲线，如图 14 所示。对锯齿区，
z
光滑弹在侵彻初期形成正向的接触力矩，后期形成反向的接触力矩；而锯齿弹主要形成正向的接触力
矩，如图 14（a）所示。这说明锯齿弹与光滑弹在该区域与靶体的作用机理不同。对非锯齿区，在大约前

1 200 mm 侵彻深度内，锯齿弹接触力矩总体上稍大于光滑弹，且两者总体为正值；在剩余侵彻过程中，两
者接触力矩的大小都有较大的波动，其中锯齿弹接触力矩总体为负值，如图 14（b）所示。当将锯齿区与
非锯齿区的接触力矩合成后，锯齿弹总体接触力矩峰值大于光滑弹，发生时间明显滞后于光滑弹，且接
触力矩脉宽更宽，如图 14（c）所示。这说明侵彻过程中锯齿弹将发生更大的偏转，这与图 7（c）中偏转角
的变化情况一致。此外，还可以发现，锯齿弹总体接触力矩峰值大于光滑弹，随着初始攻角的增大，两种
弹型接触力矩峰值均增大。当初始攻击为 3°时，锯齿弹总体接触力矩峰值仅为光滑弹的 1.1 倍，因而作
用在锯齿弹上的最大力矩与光滑弹相当。这说明在限定小攻角范围内，若结构设计能够保证光滑弹不
发生结构弯曲，则也可保证锯齿弹不发生结构弯曲。

100
80
80
60 40
40 0
M z /(kN⋅m) −20 0 Smooth, θ=1° M z /(kN⋅m) −40 Smooth, θ=1°
20

Smooth, θ=3°
−40 Smooth, θ=2° −80 Smooth, θ=2°
Smooth, θ=3°
−60 Serrated, θ=1° Serrated, θ=1°
Serrated, θ=2°
−80 Serrated, θ=2° −120 Serrated, θ=3°
Serrated, θ=3°
−100
0 200 400 600 800 1 000 1 200 1 400 1 600 0 200 400 600 800 1 000 1 200 1 400 1 600
δ x /mm δ x /mm
(a) Part AB (b) Part others
150
100

M z /(kN⋅m) 50 0
Smooth, θ=1°
Smooth, θ=2°
−50 Smooth, θ=3°
Serrated, θ=1°
Serrated, θ=2°
−100
Serrated, θ=3°
0 200 400 600 800 1 000 1 200 1 400 1 600
δ x /mm
(c) All parts
图 14 不同攻角时两种弹型锯齿区与非锯齿区接触力矩的对比
Fig. 14 Comparison of contact moments between serrated and non-serrated areas for different attack angles

051001-12