Page 11 - 《爆炸与冲击》2025年第5期

θ=2°
θ=3°
θ=1°
−100
θ=2°
−1
θ=3°
12
−150
⋅
θ=2°
− − θ=1° −1 ⋅ 16 θ=1°
θ=3°
θ=1°
− θ=2°
θ=3°
−
10 12 14 10 12 14
第 45 卷 王 帅，等： 锯齿外形对弹体带攻角侵彻横向过载的影响 第 5 期

40
5
35
0
30
−5
A s /(mm⋅ms −2 ) 20 Smooth, θ=1° A t /(mm⋅ms −2 ) −10 Smooth, θ=1°
25
−15
Smooth, θ=2°
Smooth, θ=2°
15
10 Smooth, θ=3° −20 Smooth, θ=3°
Serrated, θ=1°
Serrated, θ=1°
Serrated, θ=2° −25 Serrated, θ=2°
5
Serrated, θ=3° −30 Serrated, θ=3°
0
−35
0 2 4 6 8 10 12 14 0 2 4 6 8 10 12 14
Time/ms Time/ms
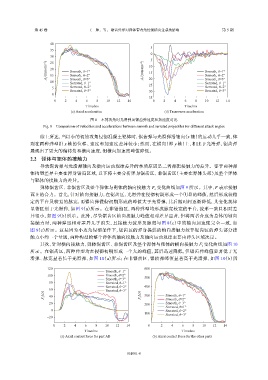
(c) Axial acceleration (d) Transverse acceleration
图 8 不同攻角时光滑弹及锯齿弹速度和加速度对比
Fig. 8 Comparison of velocities and accelerations between smooth and serrated projectiles for different attack angles
综上所述，当以小的初始攻角侵彻混凝土靶体时，锯齿弹与光滑弹沿轴向（x 轴）的运动几乎一致，体
现在两种弹型沿 x 轴的位移、速度和加速度差异较小；然而，在横向（即 y 轴）上，相比于光滑弹，锯齿弹
展现出了更大的偏转角和横向速度，但横向加速度峰值降低。

2.2 弹体与靶体的接触力
导致锯齿弹与光滑弹轴向及横向运动规律差异的本质原因是二者弹靶接触力的差异。鉴于两种弹
体构型差异主要在弹身锯齿区域，以下将主要分析弹身锯齿区、非锯齿区（主要在弹体头部）及整个弹体
与靶体的接触力的差异。
弹体锯齿区、非锯齿区及整个弹体与靶体的轴向接触力 F 变化曲线如图 9 所示。其中，F 表示接触
s
面上的合力。首先，针对轴向接触力，在锯齿区，光滑弹在侵彻初期形成一个明显的峰值，然后形成较稳
定的平台及较宽的脉宽，而锯齿弹侵彻初期形成的峰值大于光滑弹，其后随时间逐渐降低，其变化规律
显著区别于光滑弹，如图 9（a）所示。在非锯齿区，两种弹型均形成脉宽较宽的平台，波形一致且相对差
异很小，如图 9（b）所示。此外，尽管锯齿区轴向接触力峰值相对差异显著，但将两者合成为总体的轴向
接触力时，两种弹型相对差异几乎消失，且接触力波形及脉宽与图 8（c）中的轴向加速度完全一致，如
图 9（c）所示。这是因为小攻角侵彻条件下，锯齿区的弹身提供的轴向接触力较非锯齿区的弹头部分接
触力小约一个量级，两种构型的整个弹体的轴向接触力及轴向运动规律主要由弹头区域决定。
其次，针对横向接触力，弹体锯齿区、非锯齿区及整个弹体与靶体的横向接触力 F 变化曲线如图 10
t
所示。在锯齿区，两种弹型均在侵彻初期形成一个大的峰值，其后迅速降低，但锯齿弹峰值显著低于光
滑弹、脉宽显著长于光滑弹，如图 10（a）所示；在非锯齿区，锯齿弹峰值显著高于光滑弹，如图 10（b）所

120 600
Smooth, θ=1°
100 Smooth, θ=2° 500
Smooth, θ=3°
80 Serrated, θ=1°
Serrated, θ=2° 400
60 Serrated, θ=3°
F s /kN 40 F s /kN 300 Smooth, θ=1°
Smooth, θ=2°
20 200 Smooth, θ=3°
Serrated, θ=1°
0 Serrated, θ=2°
100 Serrated, θ=3°
−20
0 2 4 6 8 10 12 14 0 2 4 6 8 10 12 14
Time/ms Time/ms
(a) Axial contact force for part AB (b) Axial contact force for the other parts

051001-8

θ
θ
θ
θ
θ
θ