Page 137 - 《爆炸与冲击》2025年第5期

第 45 卷 钱秉文，等： 超高速撞击条件下混凝土靶体内 应力波的测量和分析 第 5 期

采用验证后的数值模拟技术 [19] 对 93W 钨 表 1 弹速为 3.08 km/s 时数值模拟得到的
合金弹丸超高速打击混凝土靶板的实验进行仿 应力峰值与实验结果的对比
真分析。图 12 为 3 km/s 的撞击速度（v ）下，模 Table 1 Comparison of stress wave peaks obtained by
0
numerical simulation and experiment
拟得到的弹尾速度、弹靶界面速度、弹靶界面应
at the impact velocity of 3.08 km/s
力以及侵彻深度随时间的变化曲线，其中，v 为
应力峰值/MPa
速度，σ 为应力，h 为侵彻深度，t 为时间。参考 传感器 误差/%
实验 模拟
文献 [19]，超高速撞击过程分为 4 个阶段：短暂
P1 175.1 196 11.94
的高压初始阶段、近似的稳态侵彻阶段、第 3 侵
P2 64.1 75.6 17.94
彻阶段和回弹阶段。在稳态侵彻阶段，撞击速度
P3 34.5 39.5 14.49
为 1.7～4.0 km/s 时，随着速度的升高，侵彻深度
缓慢增大，且近似于流体动力学极限（图 13），说明弹体的侵彻类似于流体侵彻，弹靶界面应力维持在较
高状态。

3.0 Projectile tail velocity 8 9 Total depth
40 Interface velocity Quasi-steady stage
2.5 7 8 Phase three stage
30 6
2.0 5 7
v/(km·s −1 ) 1.5 σ/GPa 20 Depth of penetration 4 3 h/m h/m 6 5

1.0
10 Interface pressure 2
0.5 1 4
0 0 0 3 Hydrodynamic limit
−1 2
−20 0 20 40 60 80 100 120 140 160
t/μs 1.5 2.0 2.5 3.0 3.5 4.0
−1
v 0 /(m·s )
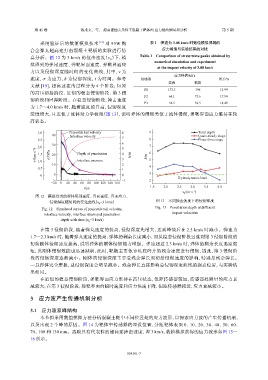
图 12 模拟得到的弹体尾部速度、界面速度、界面应力、
侵彻深度随时间的变化曲线（v 0 =3 km/s） 图 13 不同撞击速度下的侵彻深度
Fig. 13 Penetration depth at different
Fig. 12 Simulated curves of projectile tail velocity,
impact velocities
interface velocity, interface stress and penetration
depth with time (v 0 =3 km/s)
在第 3 侵彻阶段，随着弹丸速度的提高，侵彻深度先增大，达到峰值后在 2.3 km/s 时减小。弹速为
1.7～2.3 km/s 时，随着弹丸速度的提高，弹体的剩余长度减小，而从稳态侵彻阶段过渡到第 3 侵彻阶段的
初始刚体侵彻速度提高，说明弹体的刚体侵彻能力增强。弹速超过 2.3 km/s 时，弹体的剩余长度迅速缩
短，其刚体侵彻效能也迅速减弱，此时，靶板主要依靠坑底碎片的残余速度进行侵彻，因此，第 3 侵彻阶
段的侵彻深度逐渐减小。刚体的侵彻深度主要受残余弹长和初始侵彻速度的影响，特别是残余弹长。
一旦弹体完全磨损，总侵彻深度会明显减小。残余弹长直接影响总侵彻深度曲线的拐点位置，与实验结
果相同。
在近似的稳态侵彻阶段，弹靶界面应力维持在高压状态，但距传感器较远，传感器处测量的应力衰
减较大；在第 3 侵彻阶段，弹靶界面的瞬时速度和应力快速下降，但距传感器较近，应力衰减较小。

3 应力波产生传播机制分析

3.1 应力波双峰结构
本节拟采用数值模拟方法分析混凝土靶中不同位置处的应力波形，以探索应力波的产生传播机制，
以及出现 2 个峰的原因。图 14 为靶体中传感器的埋设位置，分距靶体表面 0、10、20、30、40、50、60、

70、100 和 130 mm。选取具有代表性的超高速撞击速度，即 3 km/s，数值模拟获得的应力波形如图 15～
16 所示。

054101-7